Dissertation von Dr. Peter Schmidt

zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite

3. Die Verbreitung der Hot Spots

3.1. Hot-Spot-Kataloge in der Literatur

Es hängt einerseits von der Subjektivität des Autors und andererseits von der zugrundegelegten Hot-Spot-Definition ab, ob eine vulkanische Provinz als Hot Spot erkannt wird. Die meisten Autoren liefern überdies keine Begründungen, warum sie ihre Hot Spots als solche identifizieren. Nachdem Wilson (1963) den Hot Spot anhand von Hawaii definierte, gab Morgan (1971,1972) eine 16 bzw. 20 Hot Spots umfassende Liste heraus. In der Folgezeit identifizierte man weitere Hot Spots. Diese Hot-Spot-"Inflation" gipfelte in umfassenden Listen von ca. 120 Hot Spots in Burke und Wilson (1976) oder Pollack et al. (1983). Dabei wurde in der Regel ein Zusammenhang der Hot Spots zu einem Mantel Plume gesehen. In diesem Sinne identifizierte man mehr und mehr Mantel-Plume-Hot-Spots. Inzwischen neigt man dazu, dies skeptisch zu beurteilen. Daher beziehen sich neuere Kataloge auf ca. 40 Hot Spots, für die ein Mantel Plume als Ursache angenommen werden kann, z. B. Crough und Jurdy (1980), Crough (1983a) und Richards et al. (1988). Die ältesten Hot-Spot-Listen sind sicherlich unvollständig, da manches Gebiet nicht bekannt war. Neuere Listen (ab 1980) erheben einen Anspruch auf Vollständigkeit. Allerdings ist es sehr wahrscheinlich, daß gerade die sehr umfangreichen mehr als 100 Hot Spots enthaltenden Listen nicht ausschließlich in Zusammenhang mit Mantel-Plume-Strukturen gebracht werden können.

Die Darstellungen über die weltweite Hot-Spot-Verbreitung erfolgten auf verschiedene Arten: 1. Explizit geographisch benannt wurden die Hot Spots z.B. in Wilson (1973) und Crough (1983a). 2. Die Angabe von Koordinaten machten z.B. Pollack et al. (1983) und Richards et al. (1988). 3. Die meisten Darstellungen zeigen jedoch eine Weltkarte, in der die Hot Spots durch Symbole (Punktflächen) an der jeweiligen Stelle auf der Erde eingetragen sind. Diesen Weg wählten u. a. Morgan (1971), Wilson (1973), Burke und Wilson (1976), Crough und Jurdy (1980), Vogt (1981), Pollack et al. (1981), Crough (1983a) und Pichler (1985).

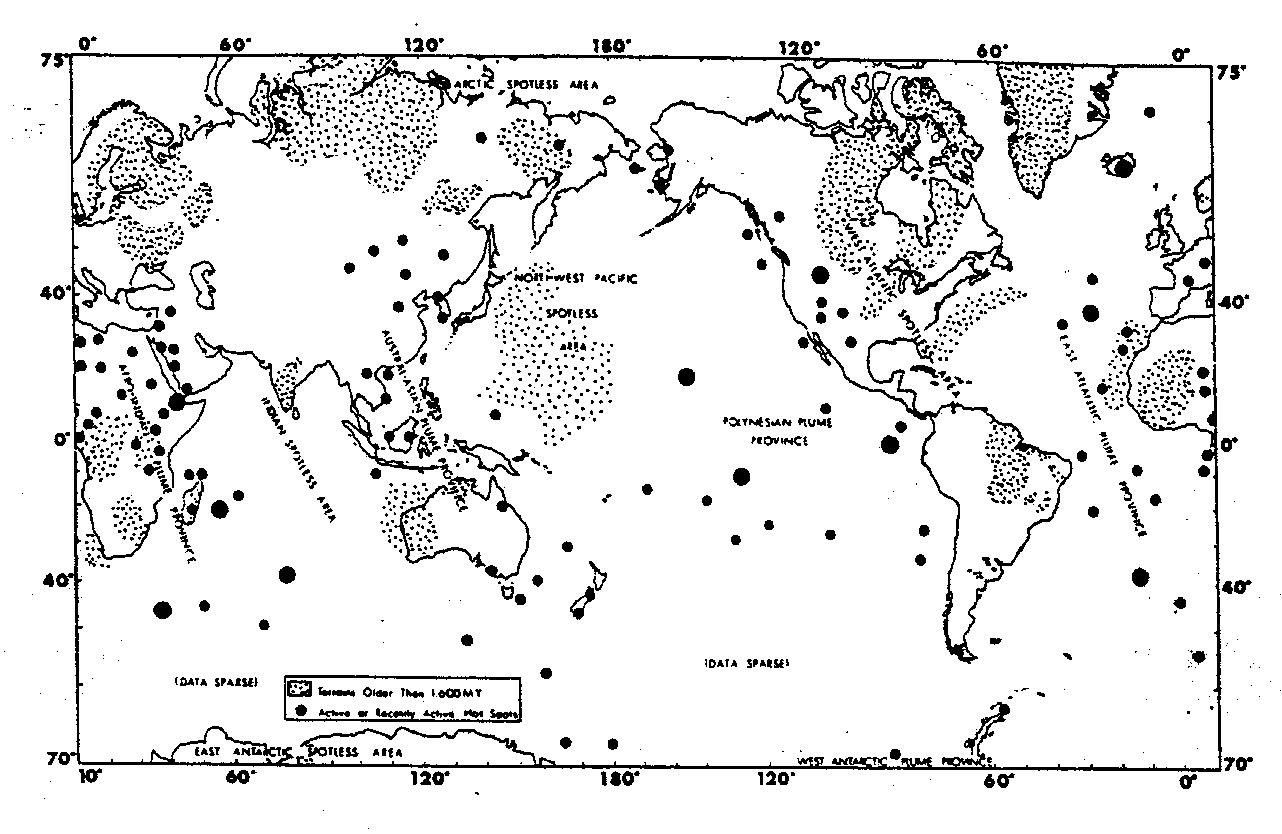
Abb. 6. Geographische Verbreitung der Hot Spots nach Vogt (1981). Die schwarzen Punkte markieren Hot Spots. Vogt (1981) unterscheidet dabei zwei Hot-Spot-Größenklassen. Punktierte Flächen stellen im Bereich der Kontinente Gebiete, die älter als 1,6 Milliarden Jahre sind, und im Bereich der Ozeane Gebiete mit einem Litho- sphärenalter von etwa 110 Millionen - 180 Millionen Jahre dar.

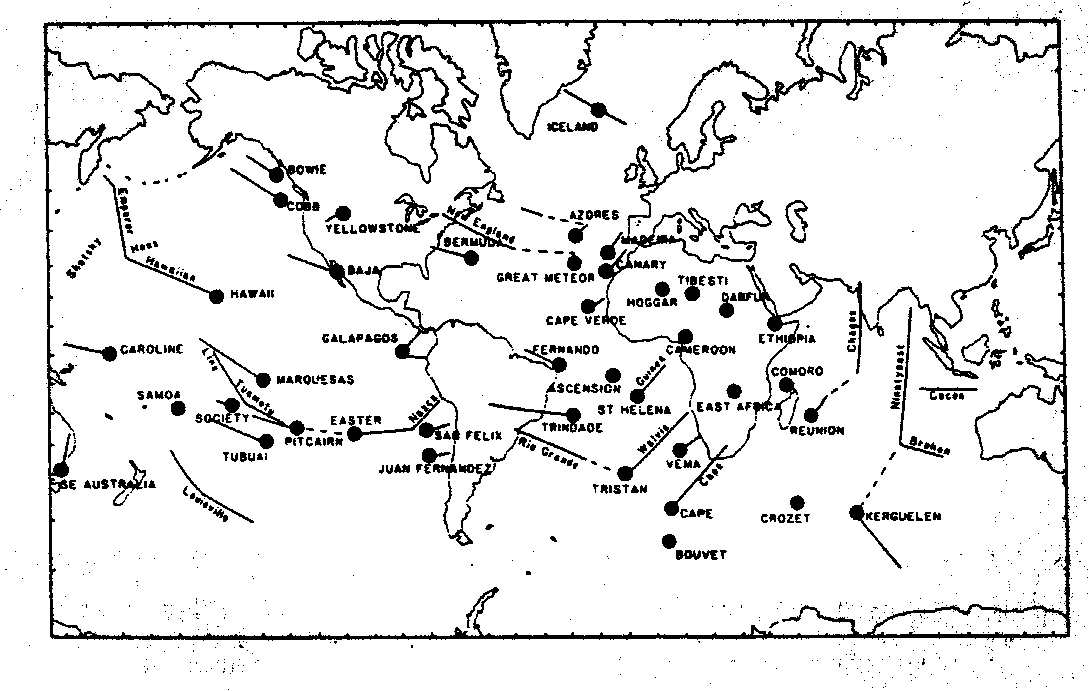
Abb. 7. Geographische Verbreitung der Hot Spots (Punkte) und Hot-Spot- Spuren (Linien) nach Crough (1983a).

Die Auflistungen kann man in zwei Kategorien unterteilen: Listen mit mehr als 100 Hot Spots und solche mit etwa 45 Hot Spots. Typische Hot-Spot-Kataloge mit mehr als 100 Hot Spots sind die von Burke und Wilson (1976) und von Pollack et al. (1983), im folgenden als Katalog 1 bezeichnet. Ein typischer Hot-Spot-Katalog mit etwa 45 Hot Spots ist derjenige von Crough (1983a) oder der von Richards et al. (1988), im folgenden als Katalog 2 bezeichnet. Die geographische Verbreitung der Hot Spots dieser beiden Listen zeigen die Abb. 6 und Abb. 7.

Im wesentlichen sind die Hot Spots nach Crough (1983a) in der Liste nach Burke und Wilson (1976) enthalten. Beide Hot-Spot-Kataloge zeigen Konzentrationen im afrikanischen und pazifischen Raum sowie die Hot-Spot-freien Gebiete Ostamerikas und Westeurasiens. Die Anzahldichte der Hot Spots nach Burke und Wilson (1976) übersteigt überall die von Crough (1983a). Darüber hinaus zeigen Burke und Wilson (1976) im Gegensatz zu Crough (1983a) Hot-Spot-Konzentrationen im ostasiatischen Raum. Aus dieser ersten Bestandsaufnahme gängiger Hot-Spot-Listen kann folgender Schluß gezogen werden: Umfangreichere Hot-Spot-Listen, für die die von Burke und Wilson (1976) repräsentativ ist, zeigen wohl unabhängig von ihrer Ursache identifizierte Hot Spots. Listen, die mit der von Crough (1983a) vergleichbar sind, konzentrieren sich dagegen auf vermutete Mantel-Plume-Hot-Spots.

3.2. Beschreibung der Hot-Spot-Verbreitung durch Felder

3.2.1. Zielsetzung und herkömmliche Methodik

Die Lage der Hot Spots auf der Erdoberfläche wird durch die Angabe von geographischen Koordinaten beschrieben. Damit liegen für die mathematische Beschreibung diskrete Punkte auf einer sphärischen Oberfläche vor. Zur besseren Korrelation mit globalen Feldern geophysikalischer Parameter wie z. B. Geoid wird es hilfreich, eine kontinuierliche Funktion zu finden, die die Hot-Spot-Verteilung gut beschreibt. Eine solche Funktion läuft auf eine Art Hot-Spot-Dichte hinaus. Die Korrelation einer Hot-Spot-Verteilungsfunktion mit geophysikalischen Globalfeldern dient dazu herauszufinden, 1. welche Hot Spots mit tieferen Ursachen, die sich z. B. im langwelli- gen Geoid manifestieren, korrelierbar sind, 2. wie groß der "Einzugsbereich" eines Hot Spots sein kann, 3. welche Hot Spots als Mantel-Plume-Hot-Spots anzusprechen sind, 4. unter welchen Voraussetzungen eine geographische Separierung dicht beieinander liegender Hot Spots noch bzw. nicht mehr vertretbar ist.

Den Versuch einer Beschreibung der Hot-Spot-Verteilung mittels Dichtefunktionen unternahmen auch bereits andere Autoren. So geben Stefanik und Jurdy (1984) Darstellungen für die Hot-Spot-Kataloge 1 und 2 an (Abb. 8). Die Schwierigkeit der Umsetzung einer diskreten Verteilung in eine Dichteverteilungsfunktion besteht in der geeigneten Wahl der Normierungsfläche. Keine der bisherigen Publikationen enthält Angaben darüber, warum diese oder jene Normierungsfläche benutzt worden ist. Wie sich in der vorliegenden Arbeit zeigt, hängt aber die Form der Ergebnisdichtefunktion in starkem Maße von der Größe der Normierungsfläche ab. Ferner werden die Ergebnisse weiterhin dadurch verfälscht, daß alle Hot Spots mit gleicher Wertung in die Funktion eingehen. Auf diese Weise lassen sich recht willkürlich gute Korrelationen mit anderen Feldern erlangen, die aber nur bedingt gerechtfertigt sind. Eine weitere Verbesserung der Korrelation wird dann oft noch durch die Entwicklung von Kugelflächenfunktionen angestrebt, da sich hier je nach Zielsetzung "lokale oder regionale Anteile" der Feldstruktur betonen lassen.

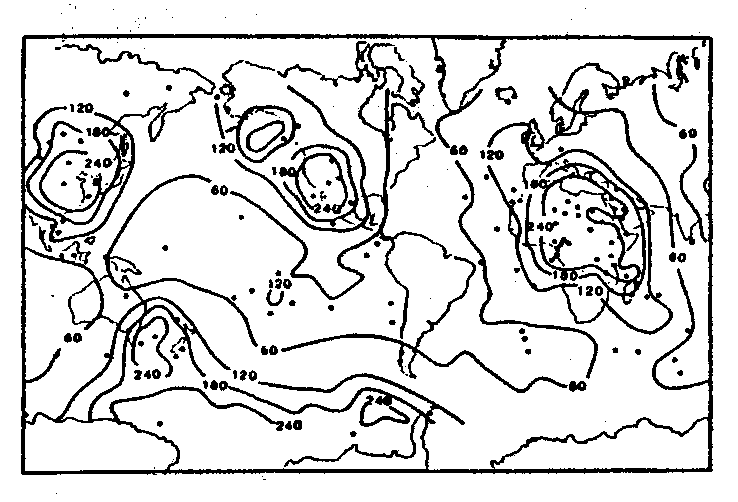
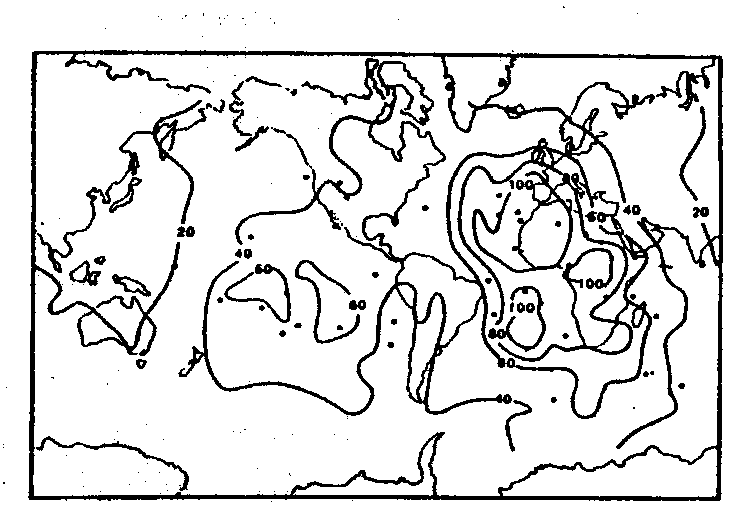
Die in Abb. 8a gezeigte Hot-Spot-Verteilungsfunktion zeigt eine unverhältnismäßig hohe Dichte im nordamerikanischen, afrikanischen und ostasiatischen Raum, wohingegen der traditionell als mit einer größeren Hot-Spot-Dichte bestückt geltende pazifische Raum stark unterrepräsentiert ist, was daran zu erkennen ist, daß der Südpazifik nach Abb. 8 eine gleiche Hot-Spot-Dichte wie die der Hot-Spot-freien Zonen nach Abb. 6 oder Abb. 9 aufweist. Dies hat seine Ursachen im wesentlichen in der für alle Hot Spots gleichen Gewichtung. Diese wird z. B. schon fragwürdig bei dem Gedanken an verschiedene Ursachen für Hot Spots oder der Möglichkeit verschiedener Hot-Spot-Intensitäten. Um ein besseres Maß für die Hot-Spot-Verteilung zu bekommen, wurden nachfolgend sehr elementare Ansätze verfolgt, aus denen erste Ergebnisse für die spätere Hot-Spot-Klassifizierung abgeleitet werden können.

Abb. 8. Hot Spots und Dichtefunktionen nach Stefanik und Jurdy (1984). a. Verteilung von 117 Hot Spots nach Burke und Wilson (1976), Katalog 1, b. Verteilung von 42 Hot Spots nach Crough und Jurdy (1980), Katalog 2. Die Dichtefunktionen sind in Einheiten von Hot Spots bezüglich einer Normierungsfläche, extrapoliert von einer lokalen Dichte, berechnet worden.

Aus dem diskreten Vorkommen von Hot Spots werden nun Funktionen gewonnen, die jedem Punkt der Erdoberfläche (Argument) einen Wert zuweisen. Die Erdoberfläche wird dabei in erster Näherung als kugelförmig angenommen. Mit einer Abtastrate von fünf Grad geographischer Breite und Länge werden die Funktionswerte berechnet. Daraus ergibt sich ein Datensatz von 73 x 37 Gridpunkten. Polwärts erhöht sich also die Abtastrate auf einem Breitenkreis, gemessen in Entfernungen. Dies beeinflußt jedoch nicht das Ergebnis. In die Berechnungen der vorliegenden Arbeit sind die Daten von Pollack et al. (1983) als Katalog 1 und die von Richards et al. (1988) als Katalog 2 eingegangen. Die Koordinatenliste von Pollack et al. (1983) weist teilweise erhebliche Mängel auf. Beispielsweise haben die Autoren mehrere ihrer Hot Spots aus der Kamerun-Gegend fast 1000 km zu weit südlich angegeben. Dies wurde mit Hilfe anderer Literatur korrigiert.

Zur Gewinnung der Daten der im folgenden erläuterten Verfahren wurden Programmroutinen geschrieben.

3.2.2. Entfernungen zum nächstgelegenen Hot Spot

- Das Verfahren

Zu jeder geographischen Koordinate läßt sich der nächstgelegene Hot Spot ermitteln. Die Entfernung zu diesem definiert den Funktionswert zu der Koordinate.

Die Ergebnisfunktion besitzt den Definitionsbereich der Kugeloberfläche. Sie ist stetig, aber nicht überall differenzierbar. Die nicht differenzierbaren Stellen sind die Hot-Spot-Lokationen sowie diejenigen Orte, die zwischen benachbarten Hot Spots das lokale Entfernungsmaximum markieren. Diese Orte ordnen sich längs eines verzweigten Linienmusters an.

- Die Vor- und Nachteile dieses Verfahrens

Niedrige Funktionswerte bedeuten hohe Hot-Spot-Dichten. Die höchste Dichte liegt an jeder Hot-Spot-Lokation selbst vor. Damit kommt es zu keiner Unterrepräsentation einzeln liegender, großer Hot Spots wie z. B. Hawaii. Es erfolgt also keine qualitative Dichtebeschreibung, jedoch in gewisser Hinsicht eine quantitative. Bestimmte Isolinien können als "geographische Einhüllende" eines Gebietes erhöhter Hot-Spot-Konzentration aufgefaßt werden. Damit lassen sich je nach betrachteter Isolinie in der Karte geographische Hot-Spot-Gebiete herausstellen. Im Hinblick auf die Tatsache, daß ein vermuteter Mantel Plume unter einem Hot Spot Ausmaße von bis zu ca. 1000 km im Durchmesser haben kann, besitzen potentielle Mantel-Plume-Hot-Spots auch einen gewissen "Einzugsbereich", der in der Größenordnung des Mantel Plumes zu sehen ist. Dadurch, daß mit diesem Verfahren zu dicht liegende Hot Spots sich im Rahmen von 500 km - und 1000 km - Entfernungen überlappen, ergibt sich nun die Möglichkeit, im Falle sehr dicht liegender Hot Spots zu sagen, daß diese nicht einer Mantel-Plume-Ursache zugeschrieben werden können oder aber als Teil einer Zentralaktivität einem Haupt-Hot-Spot geographisch unterzuordnen sind. Bis zu einem gewissen, vorsichtig abzuschätzenden Grad ergeben sich erste Hinweise auf eine mögliche Gewichtung einzelner Hot Spots. Dieses Verfahren liefert jedoch keine analytische Funktion. Außerdem findet dadurch, daß diese Funktion auf die Hot-Spot-Lokationen normiert ist, keine relative Abstufung einzelner Hot-Spot-Lokationen untereinander statt.

- Ergebnisdiskussion

Die wesentlichste Gemeinsamkeit von Katalog 1 (Abb. 9) und Katalog 2 (Abb. 11) ist der ähnliche Verlauf der 1000 km - Isolinie. Bedingt durch eine potentielle Mantel-Plume-Struktur mit ihren Abmessungen von bis zu 2000 km Durchmesser markiert sie den maximalen Einflußbereich eines Mantel Plumes für Mantel-Plume-Hot-Spot-Strukturen an der Oberfläche. Damit definiert sie als Einhüllende größere, zusammenhängende Hot-Spot-Gebiete. Außerdem zeigt der Vergleich von Katalog 1 mit Katalog 2 übereinstimmend die Hot-Spot-fernen und damit auch Hot-Spot-freien Gebiete im östlichen Amerika und im Bereich Indien und Zentraleurasien.

Die größten Abweichungen liegen bei den in Katalog 1 gezeigten Hot-Spot-Gebieten in Ostasien, Nordwestamerika und im antarktisch-australischen Raum, die der Katalog 2 nicht aufweist. So ist Ostasien in Katalog 2 sogar das Gebiet größter Hot-Spot-Ferne. Dadurch ist die bei beiden Katalogen auftretende übereinstimmende Zone der Hot-Spot-Ferne in Eurasien in Katalog 2 östlich verschoben worden. Die Hot-Spot-Provinzen in Ostasien, Nordwestamerika und in Europa fallen mit Gebieten zusammen, die von Subduktionsprozessen und Terrane-Angliederungen beeinflußt sind. Dies läßt ebenfalls auf andere Ursachen schließen. Beide Kataloge weisen den Hot Spot von Hawaii als einen sehr isolierten Hot Spot aus. Dieser ist am wenigsten von anderen geotektonischen Prozessen beeinflußt.

Man erkennt anhand der 500 km - Isolinie, daß für Katalog 2 im afrikanischen Raum die einzelnen Hot Spots klar auseinander liegen. Dies ist im Katalog 1 nicht der Fall. Hier finden beträchtliche Überlappungen statt. Einzelne Hot Spots gehen in der Darstellung zugunsten einer Art Häufung oder "clustering" unter. Es gibt Literatur, z. B. McHone et al. (1987), in der die dichte Lage der Hot Spots als Argument gegen die Mantel Plumes herangezogen wird. Es soll mit dieser Methode nun herausgestellt werden, daß es die dichte Lage zwar gibt, aber diese als konkreter Hinweis auf die Existenz von Hot Spots verschiedenen Ursprungs gedeutet werden muß. Mantel-Plume-Hot-Spots zu trennen, die dichter liegen als 1000 km, macht wenig Sinn. Denn ein Mantel Plume muß erst einmal die Lithosphäre "durchbrennen", bevor er in Form eines Hot Spots an der Oberfläche beobachtet werden kann. Da aber zu erwarten ist, daß kleine Mantel Plumes, die es durchaus geben mag, keine ausreichende Energie aufweisen, um sich bis zur Oberfläche "durchzubrennen", muß ein Mantel-Plume-Hot-Spot eine gewisse Mindestausdehnung aufweisen. Eine derartige Ausdehnung kann in den topographischen Schwellen, die um viele Hot Spots ausgeprägt sind, direkt beobachtet werden. Dies wird in Kap. 3.3. anhand der Abb. 20 näher erläutert.

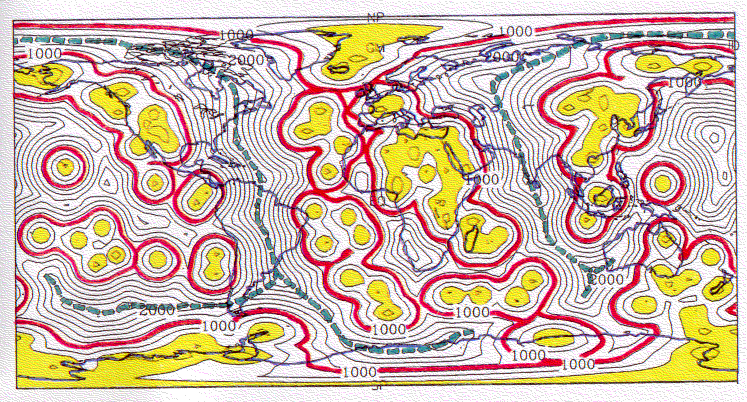
Abb. 9. Globales "Feld" der Entfernungen zum nächstgelegenen Hot Spot für den Katalog 1 mit ca. 120 Hot Spots, die Pollack et al. (1983) identifizierten. Neben den Küstenlinien der Kontinente ist folgendes dargestellt: schattiert: Bereich bis zu einer Entfernung von 500 km zu einem Hot Spot (zentrale Hot-Spot-Gebiete), durchgezogen: 1000 km - Entfernungs-Isolinie zum nächstgelegenen Hot Spot, gestrichelt: Die Linie lokaler größter Hot-Spot-Ferne. Die Bedeutung der durchgezogenen Linie ist der maximale Einzugs- bereich eines Mantel Plumes nach Abb. 5.

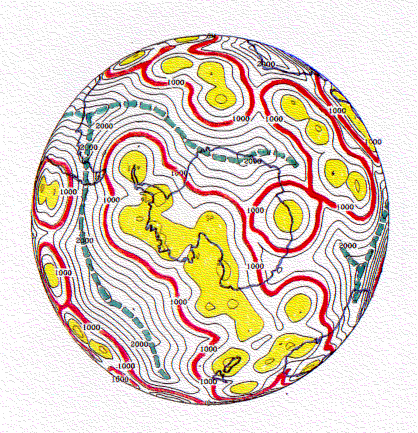
Abb. 10. Struktur der Daten aus Abb. 9 über der Antarktis, dargestellt in einer orthographischen Projektion. Es gilt die Legende von Abb. 9.

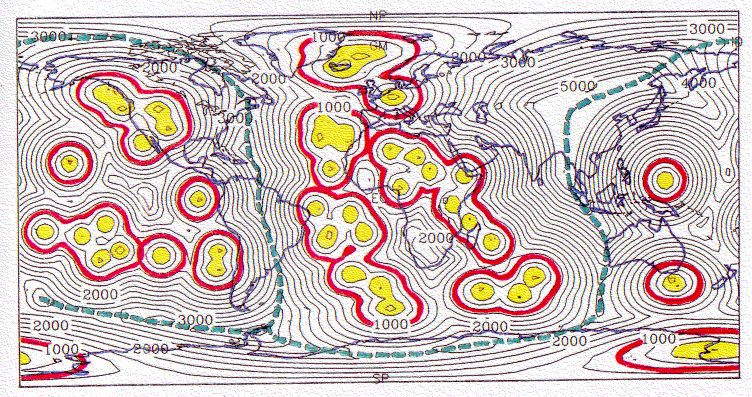
Abb. 11. Globales "Feld" der Entfernungen zum nächstgelegenen Hot Spot für Katalog 2 mit ca. 40 Hot Spots, die Richards et al. (1988) identifizierten. Neben den Küstenlinien der Kontinente ist fol- gendes dargestellt: schattiert: Bereich bis zu einer Entfernung von 500 km zu einem Hot Spot (zentrale Hot-Spot-Gebiete), rot: 1000 km - Entfernungs-Isolinie zum nächstgelegenen Hot Spot, grün: Die Linie lokaler größter Hot-Spot-Ferne. Die Bedeutung der roten Linie ist der maximale Einzugsbereich eines Mantel Plumes nach Abb. 5.

Eine Unterrepräsentation des pazifischen Raumes, wie sie in Abb. 8 zu sehen ist, liegt mit diesem Verfahren nicht mehr vor. Obwohl der Katalog 1 in Polynesien zahlenmäßig weniger Hot Spots nennt als in Afrika, kommt beiden Gebieten durch die Art der Darstellung die gleiche Bedeutung in der Gewichtung zu. Eventuell noch unentdeckte Gebiete in der Umgebung bereits bekannter Hot Spots vor allem im pazifischen Raum mit geringfügigem Vulkanismus am Meeresboden, der insbesondere die in Kap. 4.3.2. anhand von Abb. 28 dargelegte geochemische Hot-Spot-Charakteristik aufweist, würden keine Veränderung der 1000 km - Isolinie liefern.

Rege Hot-Spot-Tätigkeit in der Antarktis zeigt besonders gut Abb. 10. Hier auffällig ist die beinahe lineare Anordnung. Diese Vulkanprovinzen werden in der Literatur oft im Zusammenhang mit Riftingprozessen diskutiert. Dies gibt einen weiteren Hinweis auf eine bestimmte Hot-Spot-Klasse. Diese Art gruppiert sich auch längs des afrikanischen Riftsystems.

Schließlich kann folgende, vorläufige Gebietseinteilung der Hot-Spot-Provinzen der Erde vorgenommen werden:

1. Afrika mit den Provinzen Sahara, Kamerun, Ostafr. Rift, Mascarenen, 2. Atlantik mit den Provinzen Mittelsüdatl., Nordostatl., Island, 3. Südpazifik, 4. Nordwestamerika, 5. Ostasien, 6. Antarktis-Tasmanien, 7. Südindik sowie die Einzel - Hot Spot - Gebiete Hawaii, Europa, Karolinen u. a.

3.2.3. Hot-Spot-Ansammlungen in Umkreisen

- Das Verfahren

Die betrachtete geographische Koordinate liege im Zentrum eines Gebietes der Erdoberfläche mit entsprechend der Oberfläche folgendem, gekrümmten Radius r. Es wird nun die Anzahl der im Gebiet liegenden Hot Spots ermittelt. Dies bestimmt den Funktionswert. Der Radius r (Normierungsradius) wird variiert, um eine Abschätzung über die Aussagekraft der so ermittelten Dichteverteilungsfunktionen zu erlangen.

Auch hier besitzt die Funktion die Kugeloberfläche als Definitionsbereich. Sie liefert natürliche Zahlen als Funktionswerte. Durch eine geeignete Interpolation läßt sich aber dennoch eine stetige Funktion erzeugen. Diese läßt sich dann auch überall differenzierbar definieren. Der Wertebereich der Funktion sind positive Zahlen und die Null.

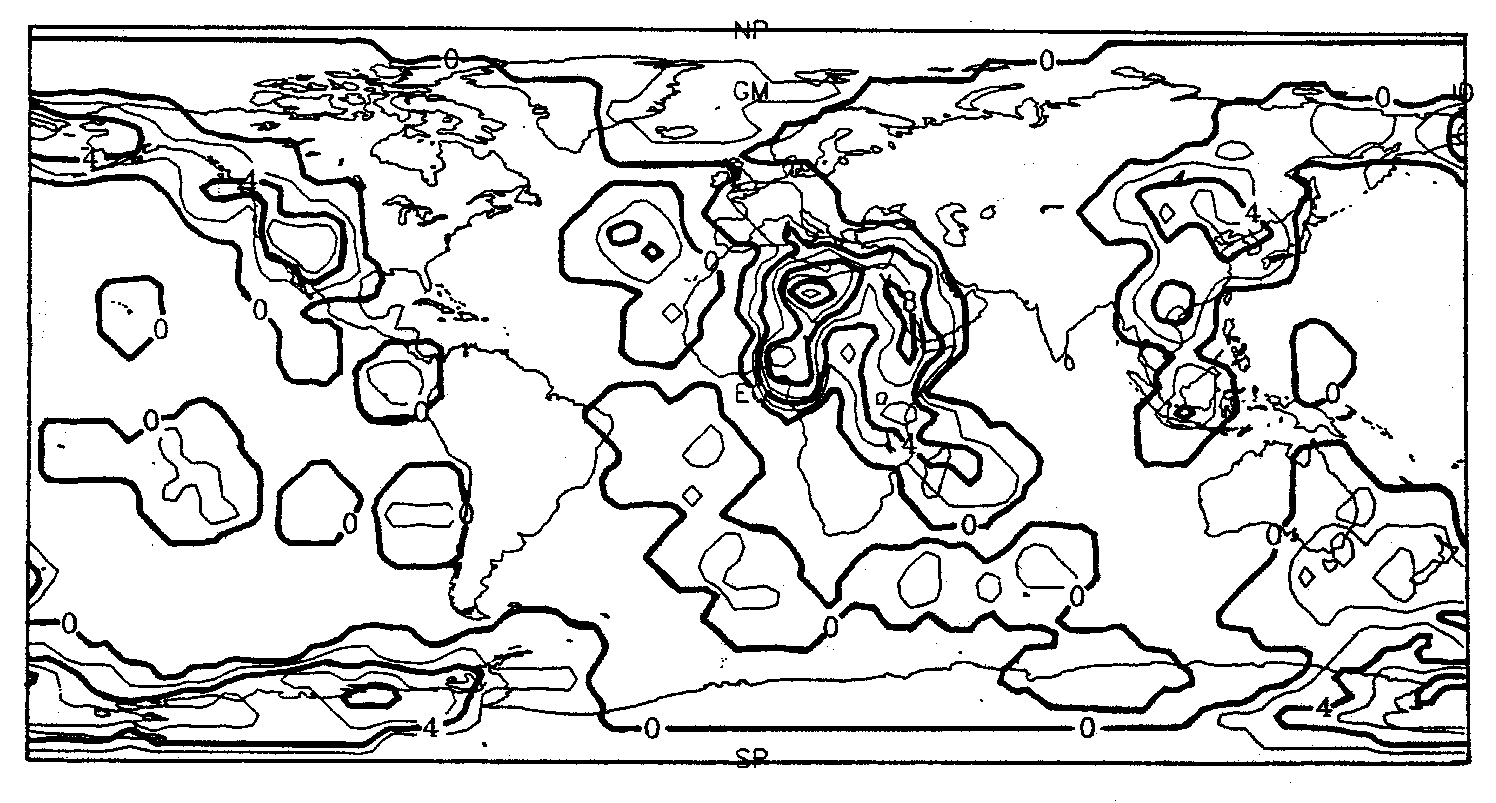
Abb. 12. Darstellung der Hot-Spot-Dichte für die 1000 km - Umkreisnorm für ca. 120 Hot Spots, die Pollack et al. (1983) identifizier- ten (Katalog 1). Bei dieser Art der Darstellung ist die Hot- Spot-Dichte nur innerhalb einer Entfernung von 1000 km zum nächstgelegenen Hot Spot positiv definiert. Daher entspricht der 1000 km - Linie aus Abb. 9 hier die Nullinie.

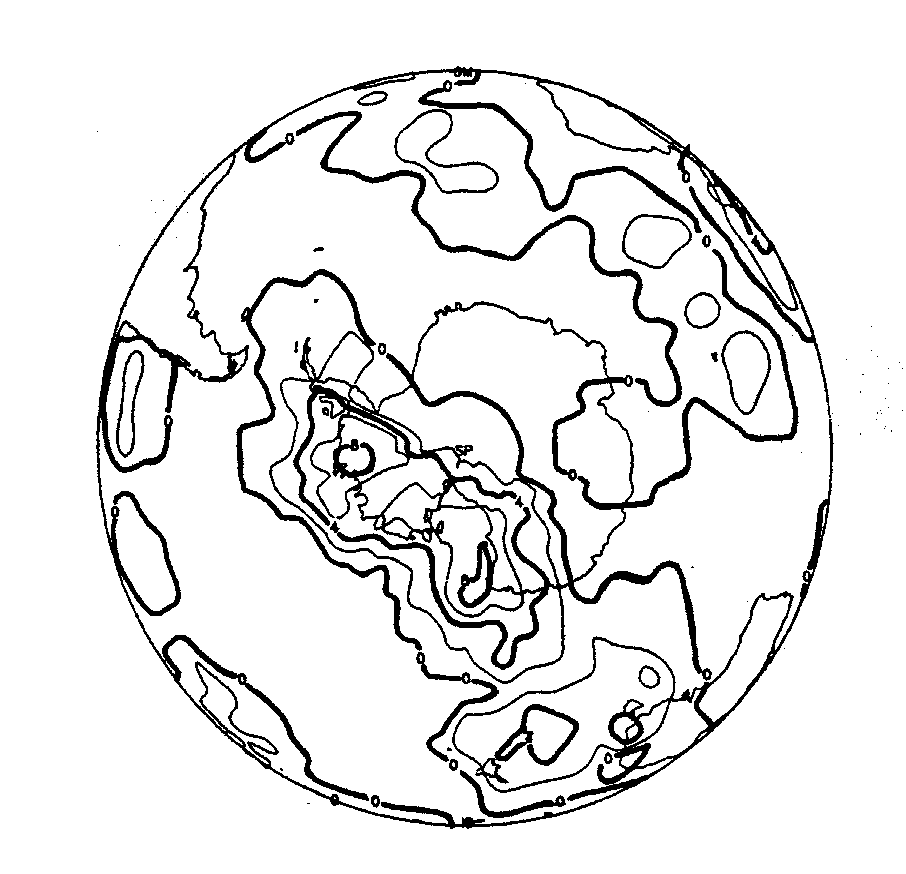
Abb. 13. Struktur der Daten aus Abb. 12 über der Antarktis, dargestellt in einer orthographischen Projektion.

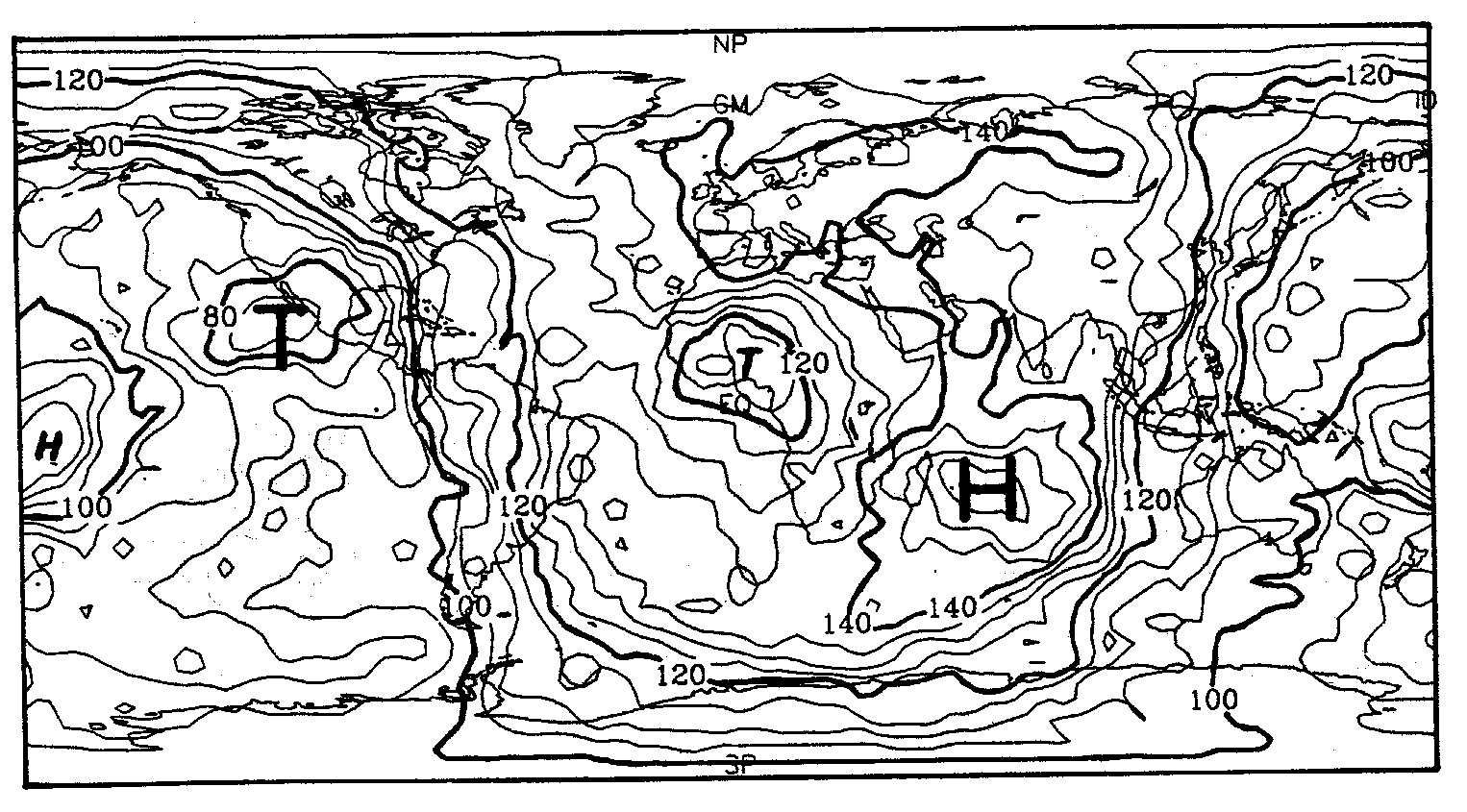
Abb. 14. Darstellung der Hot-Spot-Dichte der Hot Spots nach Pollack et al. (1983) für die 10000 km - Umkreisnorm (Katalog 1). Das H (Hoch) steht für viele und das T (Tief) für wenige Hot Spots.

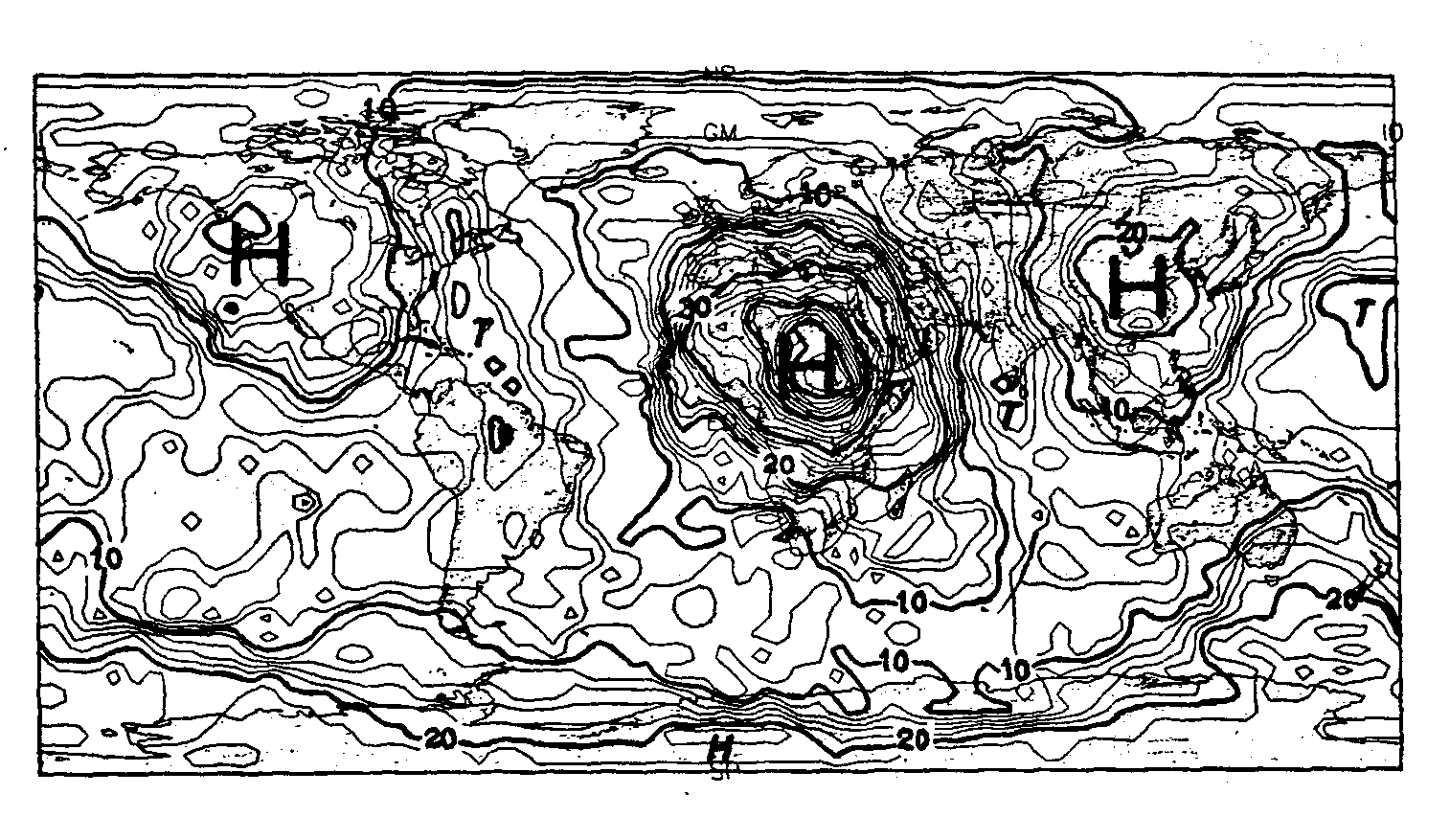
Abb. 15. Darstellung der Hot-Spot-Dichte für die 3000 km - Umkreisnorm für ca. 120 Hot Spots, die Pollack et al. (1983) identifizier- ten (Katalog 1).

Die Höhe des Betrages der Maxima dieser Funktion werden durch den Einzugsradius r, welcher noch als Parameter enthalten ist, bestimmt. Für Werte des Parameters r, die unterhalb des absoluten Maximums der Entfernungsfunktion aus Kap. 3.2.2. liegen, existieren Bereiche, in denen der Wert der Umkreis (r) - Funktion verschwindet.

Durch den Parameter r wird die Normierungsfläche definiert, innerhalb der die dort liegenden Hot Spots gezählt werden. Geht r gegen Null, d. h. mit dem Verkleinern der Fläche, spiegelt die Funktion die diskrete Verteilung wider. Umfaßt die Normierungsfläche die gesamte Erdoberfläche, so erhält man einen überall gleichen Funktionswert. Diese beiden Extremfälle begrenzen die Arten der Beschreibung durch eine Dichtefunktion. Die Wahl der geeigneten Normierungsfläche durch den Radius r hängt von dem ab, was die Funktion herausarbeiten soll. Wünschenswert ist ein Ergebnis, das Minima in Bereichen größter Hot-Spot-Ferne und Maxima in Bereichen größter Hot-Spot-Konzentrationen aufweist.

- Die Vor- und Nachteile dieses Verfahrens

Dieses Verfahren ähnelt sehr den bisherigen, von anderen Autoren beschrittenen Wegen, die mit einer Referenzfläche zur Normierung argumentierten. Aus der im Verhältnis zur Verfügung stehenden Fläche sehr dünnen Hot-Spot-Population läßt sich sehr schwer eine befriedigende Lösung für eine Dichtefunktion angeben. Betrachtet man nur einen Normierungsradius, so treten diejenigen Probleme wie in Abb. 8 auf. Die Hot-Spot-Dichte erscheint in einigen Gebieten erhöht, in anderen Gebieten zu niedrig. Massive Hot Spots, die wie Hawaii nahezu nachbarfrei liegen, verlieren zugunsten einer Ansammlung kleiner, aber geographisch dicht liegender Vulkantätigkeit an Wichtigkeit.

- Vergleichende Ergebnisdiskussion

Die Wahl von r = 1000 km (vgl. Abb. 12 und Abb. 16a) zeigt die im Entfernungsverfahren durch die 1000 km - Isolinie eingehüllten Hot-Spot-Gebietsprovinzen nun durch die Isolinie 0. Die Hot Spot-Konzentration innerhalb dieser Gebiete ist für Katalog 1 gut wiedergegeben worden. Das bestätigt auch die Abb. 13 für die Antarktis. Die Wiedergabe einer guten Dichtefunktion hängt neben r auch noch von der Gesamtanzahl der diskreten Hot-Spot-Lokationen ab. Je größer diese ist, desto besser kann die Dichte beschrieben werden. Für Katalog 2 ist die Hot-Spot-Anzahl für r = 1000 km zu gering, um eine sinnvolle Dichtefunktion zu erzielen. Jedoch weist

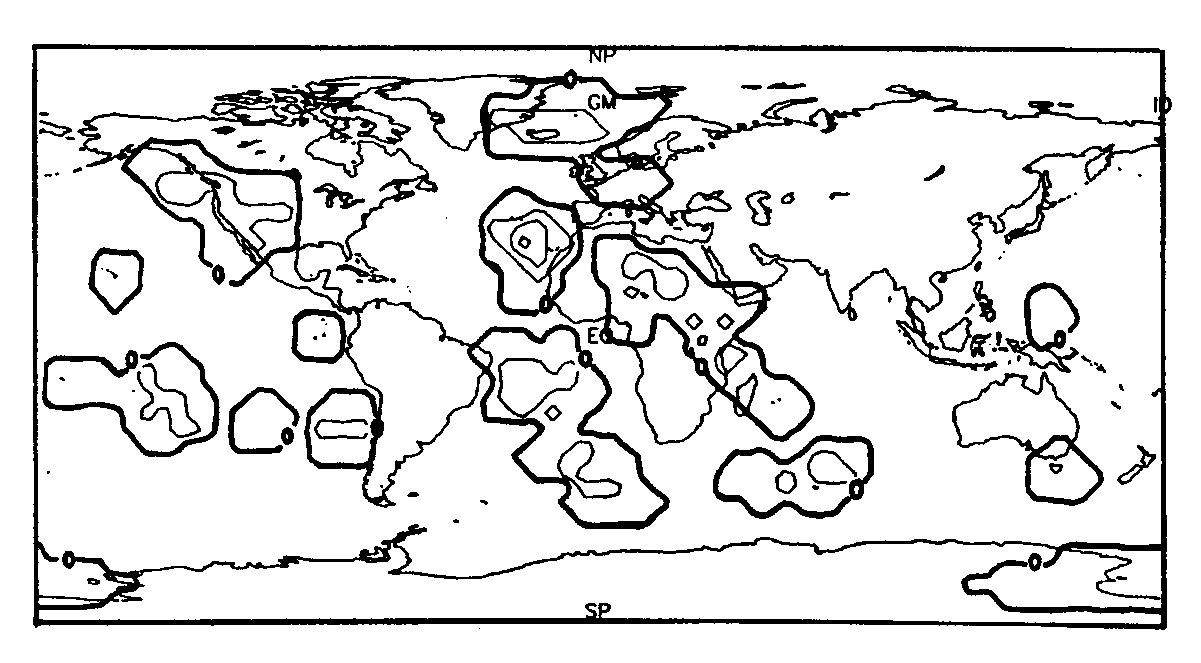
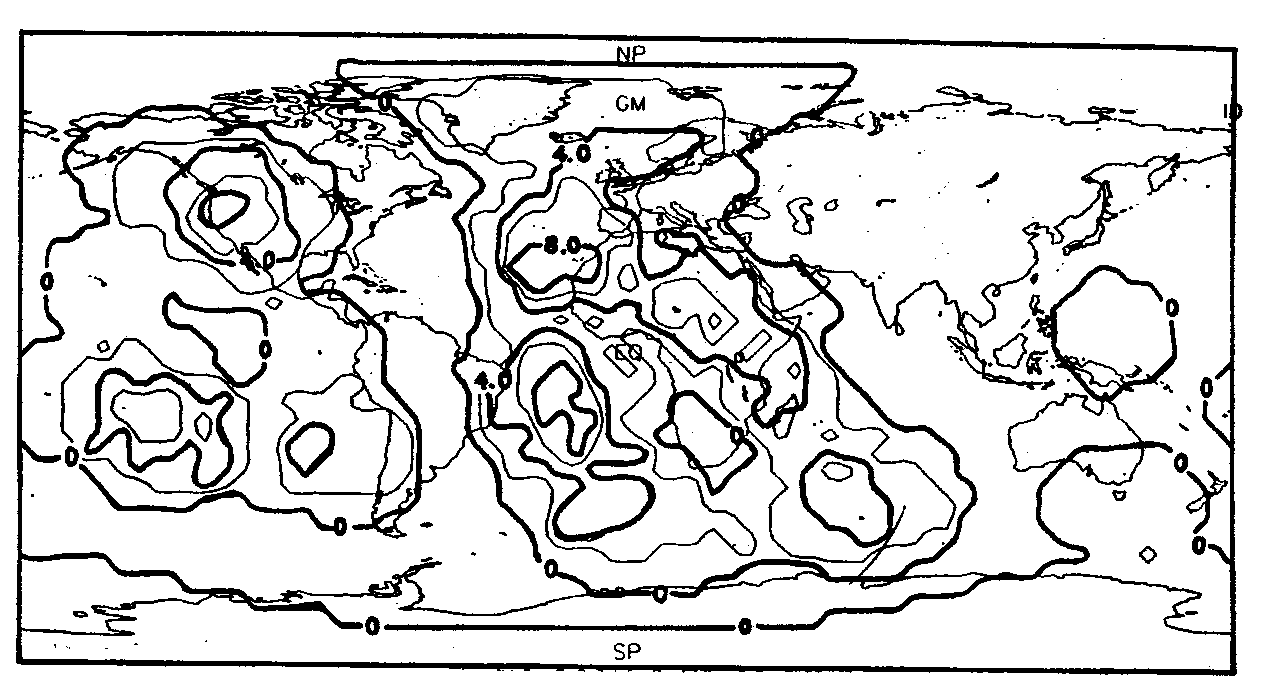
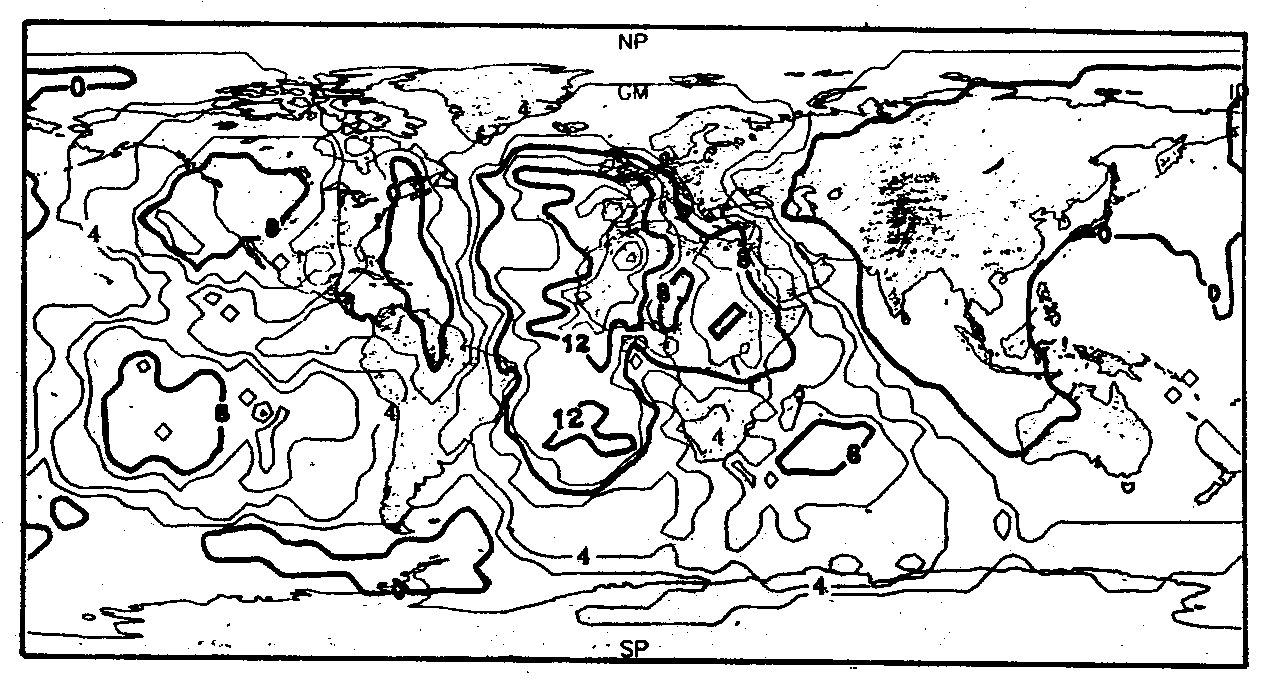
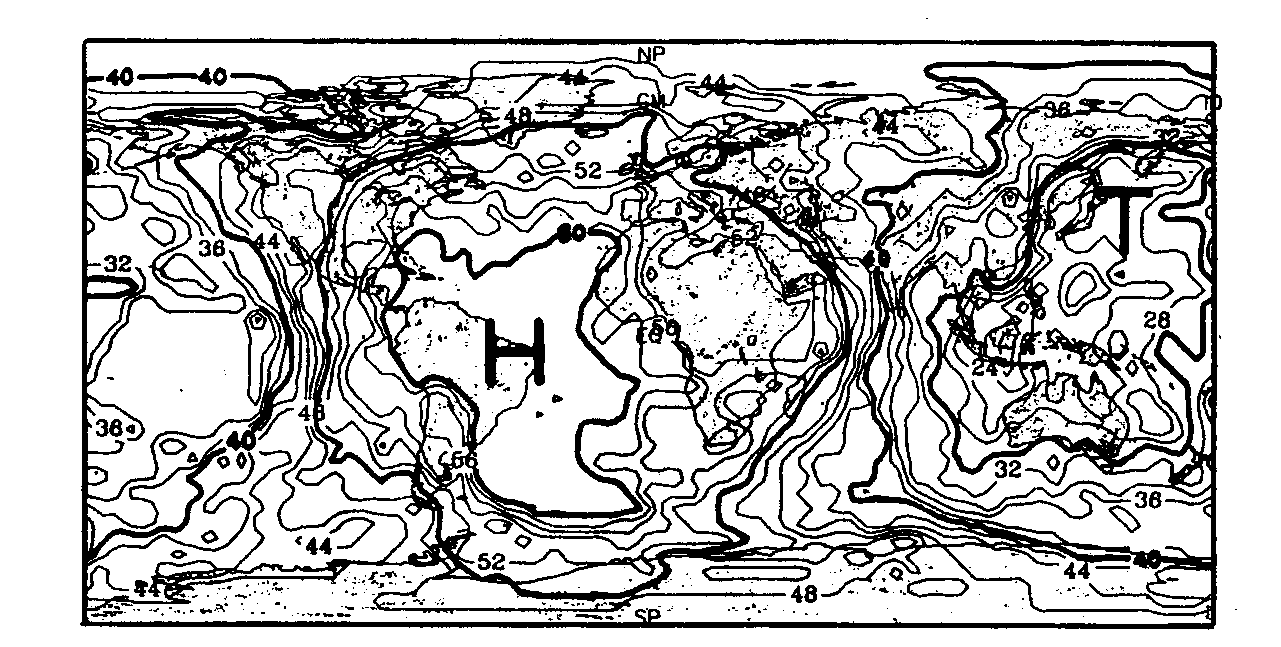
Abb. 16. Darstellung der Hot-Spot-Dichte für verschiedene Normierungsra- dien für die ca. 40 Hot Spots (Katalog 2), die Richards et al. (1988) identifizierten. a. r = 1000 km, b. r = 2000 km, c. r = 3000 km und d. r =10000 km.

auch Abb. 12 für diejenigen Gebiete, die in einer größeren Entfernung als r vom nächsten Hot Spot liegen, keine wohldefinierte "Dichte" mehr auf. Hier verschwindet der Funktionswert. Dies kann durch zwei Möglichkeiten geändert werden: a. durch die Wahl eines größeren r oder b. durch eine Kombination der Ergebnisse aus dem Entfernungs- verfahren mit der Dichtefunktion.

a. Abb. 16 zeigt die Veränderung des Parameters r für Katalog 2. Hier erkennt man deutlich, daß für niedrige r eine Beschreibung der "lokalen, also kurzwelligen" Anteile und für größere r eine zunehmende Beschreibung der "regionalen, also langwelligen" Anteile realisiert werden kann. Den besten Charakter einer Dichtefunktion erzielt man mit r = 3000 km. Dies zeigen die Abb. 15 für Katalog 1 und die Abb. 16c für Katalog 2. Hier verschwindet die Darstellung der Einzugsbereiche einzelner Hot Spots hinter der Darstellung einer von Einzellokationen unabhängigen Dichtefunktion. Dies erkennt man insbesondere daran, daß beispielsweise der Hot Spot von Hawaii gänzlich in ein Gebiet schwacher Hot-Spot-Dichte fällt. Die Ergebnisse erinnern an die aus Abb. 8 gewonnenen. Sie mögen sich zwar für eine Dichtebeschreibung eignen, haben aber durch die ungeklärte Hot-Spot-Natur keinerlei physikalische Aussagekraft. Daher können sie auch nicht zu einer Klassifizierung oder Korrelation herangezogen werden. Die Abb. 16d sowie Abb. 14 analysieren die Hot-Spot-Dichte für eine hemisphärengroße Normierungsfläche. Diese Darstellungen zeigen, daß unabhängig vom Katalog die meisten Hot Spots auf der Landhalbkugel der Erde um Afrika liegen.

b. Insbesondere für Katalog 1 bietet es sich an, die Hot-Spot-Dichte mittels einer Kombination des Verfahrens mit der 1000 km - Umkreisnorm mit dem Entfernungsverfahren zu beschreiben (Abb. 17). Der Vergleich der Abb. 9 mit der Abb. 12 zeigt, daß die Isolinie 0 aus der Darstellung für die 1000 km - Umkreisnorm (Abb. 12) mit der Isolinie 1000 km aus der Darstellung der Hot-Spot-Entfernungen (Abb. 9) übereinstimmt. Der Verlauf dieser Isolinie bestimmt die Grenze zwischen Hot-Spot-nahen und Hot-Spot-fernen Gebieten. Für die Hot-Spot-nahen Gebiete gilt bei der Kombination die Funktionswertbestimmung nach der 1000 km - Umkreisnorm, für die Hot-Spot-fernen Gebiete die Funktionswertbestimmung nach dem Entfernungsverfahren. Die auf diese Weise konstruierte Dichtefunktion, welche stetig, aber längs der 1000 km - Isolinie nicht differenzierbar ist, stellt die Bereiche größerer Hot-Spot-Konzentrationen klar heraus und löst das Problem der Unterrepräsentation weniger dichter, aber dominanter Hot-Spot-Gebiete wie die des Südpazifik, weil die wirklich Hot-Spot-freien Gebiete, z. B. Ostamerika, noch um Größenordnungen niedrigere Werte zugewiesen bekommen.

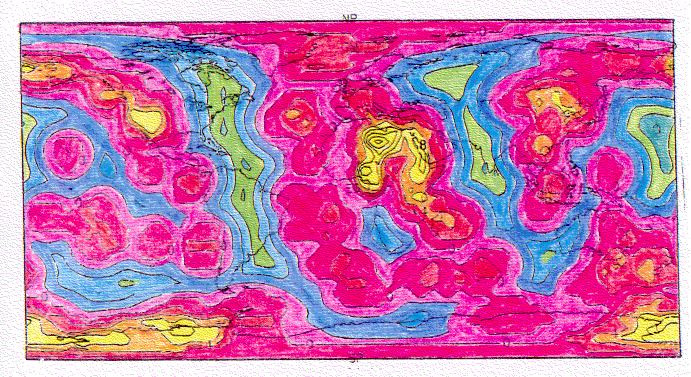
Abb. 17. Kombination der Ergebnisse aus der Entfernungsfunktion und der Dichtefunktion mit r = 1000 km für Katalog 1. Danach sind für die Gebiete bis zu einem Abstand von 1000 km die Daten aus der Abb. 12 (Hot-Spot-Dichte in dem 1000 km - Umkreis) und für die weiter als 1000 km von einem Hot Spot entfernten Gebiete die Daten aus Abb. 9 übernommen worden. Die dargestellte Abstufung von "Punktiert" nach "Schraffiert" läuft von großer zu kleiner Hot-Spot-Dichte. Dicht punktiert sind die Gebiete sehr großer Hot-Spot-Dichte. Punktierte Gebiete bezeichnen Gebiete mit grö- ßerer Hot-Spot-Dichte. Die schraffierten Gebiete, die Hot-Spot- frei sind, stellen eine graduelle Verringerung einer definier- ten Hot-Spot-Dichte dar. Die so gewonnene Beschreibung der Hot- Spot-Dichte rückt die Gebiete sehr hoher Hot-Spot-Dichte wie Afrika in den Vordergrund, ohne dabei den südpazifischen Raum, wie dies in Abb. 8a geschehen ist, mit den Hot-Spot-freien Ge- bieten, hier schraffiert dargestellt, gleichzustellen.

Die Beschreibung der Hot-Spot-Verteilung nach Abb. 17 stellt eine kontinuierliche Hot-Spot-Dichte-Funktion dar, deren Funktionswerte zwar noch von der Wahl des zugrundegelegten Hot-Spot-Katalogs, aber nicht mehr allein von der für eine Anzahldichte benutzten Größe eines Normierungsgebietes abhängen. Die Funktionsdarstellung nach Abb. 17 eignet sich für eine erste geographische Einteilung der Hot Spots. So zeigen sich im wesentlichen zwei Hot-Spot-Gebiete: der afrikanisch-atlantische Raum und der pazifische Raum. Die Hot Spots im afrikanisch-atlantischen Raum liegen allesamt im Bereich sich langsam bewegender Platten und treten oftmals in Form ganzer Vulkangruppen (z. B. Kanarische Inseln) in den Ozeanen oder ausgedehnter Vulkangebiete (z. B. Hoggar) auf den Kontinenten auf. Die Hot Spots im pazifischen Raum liegen im Bereich der sich schnell bewegenden pazifischen Platte und befinden sich oftmals am jüngeren Ende von Seamountketten progressiven Alters (vgl. z. B. Abb. 7).

Die Hot-Spot-Dichte-Funktion nach Abb. 17 belegt dicht beieinander liegende Hot-Spot-Lokationen mit hohen Werten und unterscheidet die übrigen Hot-Spot-Gebiete deutlich von Hot-Spot-freien Gebieten, so daß isoliert liegende Hot Spots nicht mit Hot-Spot-freien Gebieten gleichgesetzt werden können. Dies ermöglicht eine aussagekräftigere Korrelation der Hot-Spot-Dichte mit global vorliegenden Felddaten wie Freiluftschwere und Geoid als mit bisherigen Hot-Spot-Dichte-Beschreibungen.

3.3. Globale Korrelation physikalischer Parameter

Die Ergebnisse des vorangestellten Kapitels zeigen, daß von einer zufälligen Verteilung der Hot Spots, wie sie Crough (1978) vertritt, keineswegs die Rede sein kann. Vielmehr zeigt insbesondere Abb. 11 die hemisphärische Verdichtung der Hot Spots im Südpazifik und um Afrika, jeweils getrennt durch die Hot-Spot-freien Zonen. Dieses Phänomen erkannten auch bereits Chase (1979), Crough und Jurdy (1980), Anderson (1982) u. a. Damit ergibt sich die Möglichkeit eines Zusammenhanges von Hot-Spot-Verdichtungen zu global wirksamen Konvektionsprozessen im Erdinnern. Dies zu beleuchten, ist das Ziel der nun folgenden Überlegungen.

3.3.1. Geoid-, Schwere- und topographische Anomalien (Schwellen)

Nach Abb. 18 liegen die Hot Spots aus Katalog 2 nahezu vollständig in Gebieten mit positivem Geoidsignal, wenn die Wirkung der Subduktionszonen abgezogen wird. Lediglich für die Hot-Spot-Gebiete im westlichen Nordamerika und für die Gebiete von Bermuda und Mt. Erebus in der Antarktis trifft dies nicht zu. Chase und Sprowl (1983) fanden, daß die heutigen Geoidminima mit Regionen korrelieren, in denen vor ca. 100 Millionen Jahren Subduktion vorlag. Diese Gebiete sind heute weitgehend Hot-Spot-frei. Dies bestätigt die sehr gute Korrelation von Abb. 18 mit den Ergebnissen der Beschreibung der kontinuierlichen Hot-Spot-Verteilung in den Abb. 9, Abb. 11 und Abb. 17.

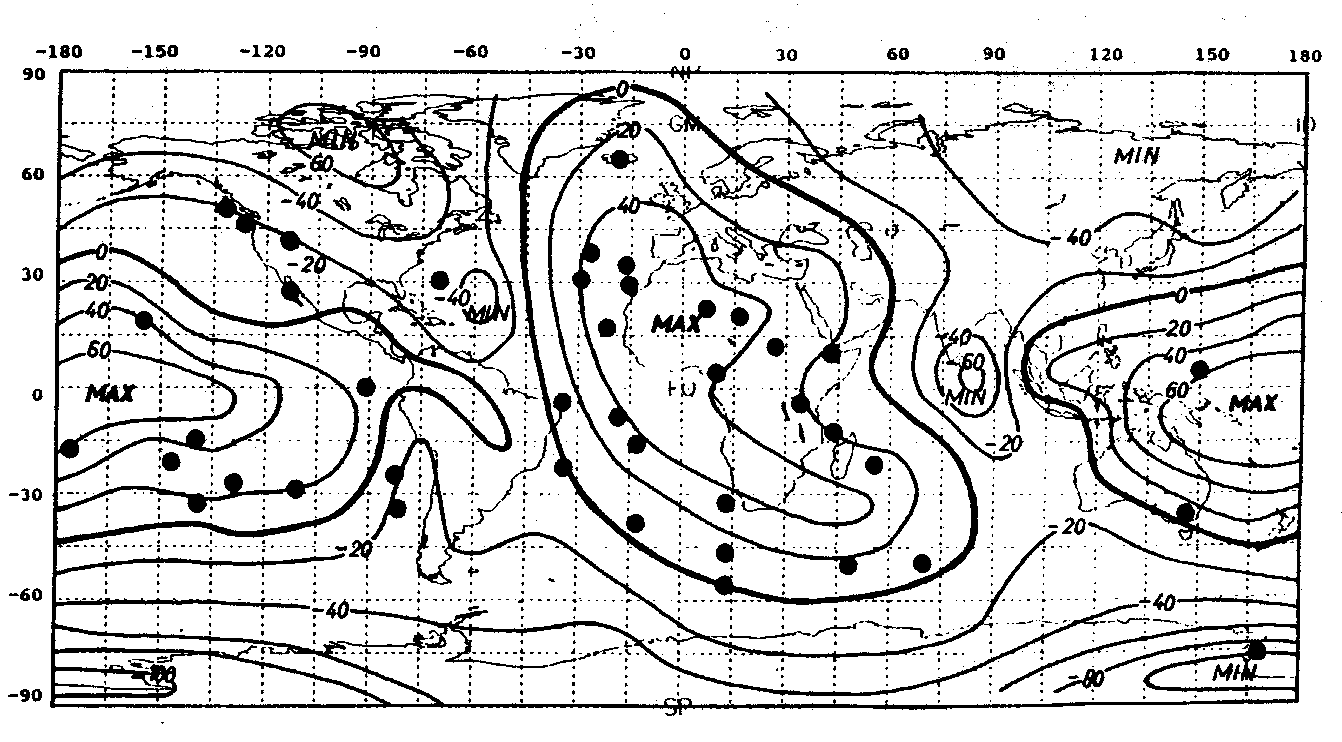
Abb. 18. Residuales Geoid, welches man nach der Subtraktion des Subduk- tionsgeoids vom totalen, beobachteten GEM 8 - (sphär.-harm. Grad 12 entsprechend einer horizontalen Auflösung im Wellen- längenbereich von etwa 3000 km)-Geoid erhält (nach Crough und Jurdy (1980)). Hot Spots nach Katalog 2 sind durch schwarze Punkte gekennzeichnet.

Vogt (1981) gibt eine Darstellung des Geoids, die mit der in Abb. 19 gezeigten Freiluftanomalie der Schwere, die im Gegensatz zu Abb. 18 den Subduktionsanteil beinhaltet, vergleichbar ist. Die Freiluftschwere und das Geoid entsprechen einander. Das Geoid enthält in erster Linie langwellige Strukturen. Diese sind auch in der globalen Freiluftschwere zu finden. Der Vergleich von Abb. 17 mit Abb. 19 zeigt, daß die Schwereminima Ostamerikas und im indisch-australischen Bereich durchaus mit Gebieten größter Hot-Spot-Ferne bzw. geringster Hot-Spot-Dichte korrelieren. Die einzige Ausnahme in dieser Hinsicht ist das Gebiet um den Mt.-Erebus-Hot-Spot. Dort liegt ebenfalls ein Schwereanomalieminimum von -25 mGal vor. Durch Schweremaxima gekennzeichnete Regionen sind insbesondere die von Subduktionsvorgängen geprägten zirkumpazifischen Gebiete. In diesen Gebieten liegen z. B. die Hot Spots Ostasiens sowie der Hot Spot von Yellowstone. Ein weiteres Gebiet mit einem Schweremaximum befindet sich z. B. südöstlich von Afrika. Dort liegen z. B. die Hot Spots Marion, Kerguelen, Crozet und andere. Auch der Island - Hot Spot liegt im Bereich eines Schwereanomaliemaximums von 25 mGal. Die allermeisten der Hot Spots liegen in Bereichen, in denen die Schwereanomalien nach Abb. 19 zwischen -5 mGal und 10 mGal liegen. So beträgt die Schwereanomalie bei Hawaii und im Südpazifik um -5 bis 5 mGal und bei Afar um 10 mGal. Es lassen sich aber auch viele Gebiete aufzeigen, die zwar eine Schwereanomalie zwischen -5 mGal und 10 mGal aufweisen, die jedoch keine Hot Spots aufweisen (z. B. Nordeuropa, Gebiete im Nordpazifik oder Arabien).

Für jede Größenordnung der Schwereanomalien lassen sich Gebiete nennen, in denen Hot Spots liegen oder in denen keine Hot Spots liegen. Damit ist keine signifikante Korrelation zwischen der Hot-Spot-Dichteverteilung nach Abb. 17 und der globalen Freiluftschwere nach Abb. 19 nachweisbar. In die Freiluftschwere gehen neben Effekten, die durch mögliche Mantel Plumes hervorgerufen sein könnten, offenbar auch sehr stark andere Eigenschaften der Lithosphäre und der Kruste ein, die über tiefere Struktursignale dominieren oder sie zumindest derartig überlagern, daß sie unkenntlich werden.

Die hier diskutierten Felder beziehen sich auf globale Ausdehnungen. Monnereau und Cazenave (1990) behandeln die Geoidstruktur im Nahbereich einzelner ozeanischer Hot Spots. Ferner gehen die Autoren auf die Meerestiefenanomalie und damit auf die topographische Struktur der Hot Spots ein. Es zeigt sich eine krustenalterabhängige Schwellenhöhe (je älter die Kruste, desto höher die Schwellenamplitude über dem aktiven Hot Spot), aber eine krustenalterunabhängige Schwellengröße. Hot Spots mit beträchtlicher Schwellenausdehnung können möglicherweise einer Mantel-Plume-Struktur zugeschrieben werden.

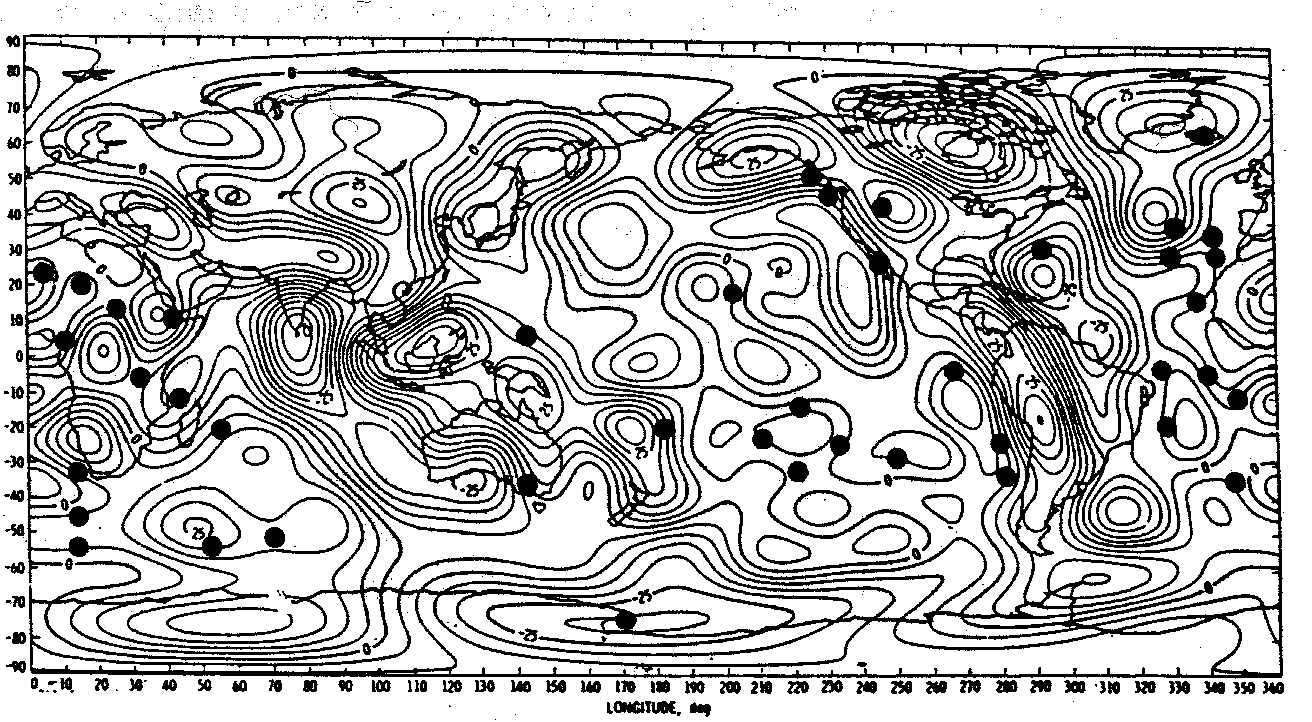
Abb. 19. Freiluftschwereanomalien der Erde, basierend auf der sphäri- schen harmonischen Entwicklung nach Lerch et al. (1979) bis zu den harmonischen Koeffizienten vom Grad und der Ordnung 16. Der Isolinienabstand beträgt 5 mGal (nach Philips und Lambeck, 1980). Hot Spots nach Katalog 2 sind durch schwarze Punkte ge- kennzeichnet.

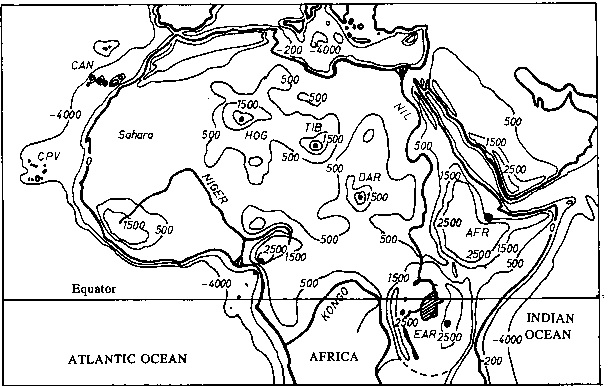
Hot Spots, die als Mantel-Plume-Hot-Spot angesprochen werden können, weisen nach den Beobachtungen von Kap. 2.2.1. eine topographische Schwelle in Form einer regionalen Aufdomung auf. Die Darstellungen aus Abb. 20a lassen den Schluß nahe, daß potentielle Mantel-Plume-Hot-Spots allesamt eine ausgeprägte regionale topographische Anomalie zeigen. Wünschenswert wäre eine globale Darstellung der Topographie, die im Hinblick auf Hot-Spot-Schwellen zu untersuchen wäre. In der Regel jedoch überlagern geologische Prozesse wie Gebirgsbildung, Sedimentation u. a. die Effekte der Mantel-Plume-Hot-Spots, so daß diese i. a. nur schwer selektierbar sind. Einen regionalen Raum neben Hawaii, der von fremden geologischen Einflüssen nicht so sehr gestört wurde, stellt der nördliche Teil von Afrika dar. Aus diesem Grunde zeigt die Abb. 20b stellvertretend für den übrigen Teil der Welt exemplarisch einige Arten der physiographischen Integration von Hot-Spot-Schwellen in regionaler Topographie. Die Landmasse Afrika wird geographisch definiert durch die 0m-Isolinie, der Bereich der kontinentalen afrikanischen Kruste wird jedoch durch den Rand des Kontinentalschelfs (-200m-Isolinie) markiert. Als Abtrennung zur Tiefsee ist die -4000m - Isolinie in Abb. 20b übernommen. Die 500m-Isolinie markiert den Übergang von Tief- zu Hochländern. Den Übergang zu den zentralen Bergmassiven markiert hier etwa die 1500m-Isolinie, die Gipfelbereiche selbst werden durch die 2500m-Isolinie dargestellt.

Die Analyse der Karte nach Abb. 20b zeigt die topographischen Schwellen der mit schwarzen Punkten markierten Hot-Spot-Lokationen durch unterschiedliche Isolinienniveaus. Im Bereich der Kanarischen und der Kapverdischen Inseln weicht die -4000m-Tiefenlinie von der Küsten- und Kontinentalrandlinie zurück. Der Meeresboden ist also um die genannten Inselgruppen flacher als er dort unbeeinflußt sein würde. Topographische Schwellen zeigen auch Hot-Spot-Lokationen im Bereich der zentralen Sahara. Die regionalen topographischen Schwellen weisen insbesondere Hoggar, Tibesti und Darfur auf. Aufgrund der Unzugänglichkeit dieser Gebiete gibt es bislang kaum Erkenntnisse über diese möglichen kontinentalen Mantel-Plume-Hot-Spot-Lokationen. Hoggar und Darfur wurden von Crough (1981a, 1981b) untersucht, Tibesti von Vincent (1970). Bei allen drei Hot Spots beträgt die regionale Aufdomung nach Abb. 20b um knapp 1000m. Einen allgemeinen Überblick über den Vulkanismus in der Sahara, der auch auf die kleineren Vulkangebiete, die nicht mit einer Schwelle assoziierbar sind, eingeht, geben z. B. Thorpe und Smith (1974). Nach Godoy (1987) läßt sich der Sahara-Vulkanismus, der im wesentlichen aus den Vulkanstöcken Hoggar, Tibesti und Darfur besteht, zu einer Hot-Spot-Familie zusammenfassen.

Sehr massive Aufdomungen, sowohl in der Wellenlänge als auch in der Amplitude (2500m) befinden sich nach Abb. 20b im östlichen Teil Afrikas. Hier befindet sich das Ostafrikanische Grabensystem. In seinem Bereich befinden sich der Kenia- (Banks und Swain, 1978) und der Afar-Dom (White und McKenzie, 1989). Das Gebiet des Afar-Doms zeigt sich als große Flutbasaltprovinz. Diese weist einen Durchmesser von weit mehr als 1000 km auf (White und McKenzie, 1989). Sleep (1990) vergleicht den Afar-Hot-Spot hinsichtlich seines subaerischen Plateaus mit Island. Hier liegt eine Kombination von Hot Spot und Rifting (Lage Islands auf der Rückenachse des Atlantiks) vor.

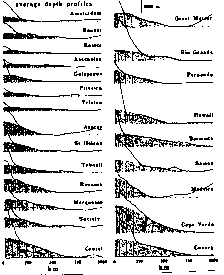
Abb. 20.a. Topographische Anomalie in Profilform (Durchschnittswerte) für 23 ausgewählte Hot-Spot-Schwellen nach Monnereau und Cazenave (1990). Die Schwellenformen (schwarze Linien) lassen sich durch Gaußkurven (schattiert) beschreiben.

b. Manuell geglättete Darstellung der topographischen Regional- strukturen des Nordteils von Afrika. Isolinien sind angegeben mit physischen Bedeutungen für -4000m: Tiefsee, -200m: Kontinentalschelf, 0m: Küstenlinie, 500m: Übergang vom Tiefland zum Hochland, Fuß der Schwellen, 1500m: Hochland, zentraler Bereich der Schwellen, 2500m: Hochland der Schwellen um das Ostafrikanische Graben- system sowie zentrale Vulkangebäude einzelner Schwel- len. Die schwarzen Punkte bezeichnen Hot Spots nach Katalog 2 (vgl. z. B. Crough, 1983a), die als potentielle Mantel-Plume-Hot- Spots ansprechbar sind.

Der nördliche Teil des Ostafrikanischen Grabens läßt sich somit durch die prägnanten Hot-Spot-Schwellen des Kenia- und Afar-Doms darstellen. Ein Zusammenhang zwischen Rifting und Mantel-Plume-Hot-Spot drängt sich damit geradezu auf. Darauf haben auch bereits White und McKenzie (1989) hingewiesen. Danach kommt es zu einem dynamischen Anheben der Kruste infolge der Einwirkung eines aufsteigenden Mantel Plumes. Dieser Vorgang hat schließlich durch Ausdünnung der Kruste die Prozesse des Riftings zur Folge.

Die Ergebnisse aus Kap. 3.2. zeigen im übrigen bemerkenswerte Ähnlichkeiten mit der Topographie des in Abb. 20b. betrachteten Raumes. Die topographische Schwelle um einen Hot Spot wird hiermit als notwendiges, aber nicht hinreichendes Kriterium zur Identifizierung von Mantel-Plume-Hot-Spots erkannt. Schwellen stellen die regionale topographische bzw. bathymetrische Anomalie dar. Eine Schwelle im ozeanischen Bereich ist insbesondere ein Gebiet mit flacherem Meeresbodenniveau als es das "standard seafloor cooling model" nach Liu und Chase (1989) erwarten läßt. Transversale Profile durch Hot-Spot-Schwellen weisen meist näherungsweise die Form einer Gaußkurve mit Spitzenamplituden von 1 bis 2 km gegenüber der Umgebung und Wellenlängen von 500 bis 2000 km auf (Liu und Chase, 1989). Hot-Spot-Schwellen umfassen 30 bis 50 % der Fläche der ozeanischen Lithosphäre (Crough, 1983a).

Hot-Spot-Schwellen zeichnen sich durch positive Geoidanomalien (6-8 m im Scheitelbereich) und möglicherweise durch eine anomale Oberflächenwärmeflußdichte (8 bis 10 mW/m2) aus (Crough, 1978; Haxby und Turcotte, 1978; Detrick et al. 1981, 1986; von Herzen et al. 1982). Von Herzen et al. (1989) können für den Hot Spot von Hawaii jedoch keine signifikante Wärmeflußanomalie feststellen (vgl. Kap. 2.2.2.2.). Die Autoren gehen auch davon aus, daß Messungen des Wärmeflusses an anderen Hot Spots, z. B. an den Kapverden durch Courtney und White (1986), fehlerhafte bzw. zu hohe Wärmeflußanomaliewerte ergeben haben. Damit würden die Hot Spots möglicherweise doch nicht anhand einer signifikanten Wärmeflußanomalie identifizierbar sein. McNutt und Shure (1986) haben Hot-Spot-Schwellen durch erhöhte Temperaturen in einer "Konvektionsschicht", die mit einem Mantel Plume vergleichbar ist, und als thermische "Expansion" in einem durch Wärmeleitung geprägten Bereich innerhalb der Lithosphäre modelliert. Die daraus mit Hilfe einer linearen Filtertechnik errechneten Kompensationstiefen für Schwellen liegen nach McNutt und Shure (1986) zwischen etwa 45 und 70 km. Da die (Intraplatten-) Schwellen nicht durch thermische Abkühlung oder lithosphärische Störungen oder Deformationen erklärbar sind, müssen sie als Folge von Prozessen im Mantel betrachtet werden (Dietz und Menard, 1953; Crough, 1978; Detrick und Crough, 1978). Theorien zu Ursachen der Schwellenbildung werden in Kapitel 7.1. im Rahmen der Erstellung eines 3D-Dichtemodells für Hawaii näher betrachtet.

Die großen Wellenlängen des Geoidsignals repräsentieren möglicherweise tiefere Ursachen im Mantel. Geoidsignalmaxima liegen im afrikanischen und pazifischen Raum. Möglicherweise spricht dies für das Vorhandensein von Konvektionssystemen globalen Ausmaßes. Danach gäbe es die zwei Zentren aufstrebenden Materials "Afrika" und "Pazifik". Damit wäre eine quadrupolare Konvektion (Busse,1983) als Strömungsmuster 1. Ordnung (global dominant) gegeben. Im Zusammenhang mit der Wechselwirkung Kruste-Mantel können Strömungsmuster 2. Ordnung (regional dominant) und 3. Ordnung (lokal dominant) auftreten.

3.3.2. Hot Spots und die Verletzbarkeit der Lithosphäre

Unter Lithosphäre wird im allgemeinen der starre Teil der äußeren Schale eines terrestrischen Planeten verstanden (Janle und Meissner, 1986). Starr ist hierbei im Sinne von bruchfähig unter Stressbedingungen zu verstehen. Die starre Lithosphäre zeigt dabei in gewisser Hinsicht ein elastisches Verhalten (z. B. Rückschwingen von Material nach einem Bruch in eine "unverbogene" Position (Stressabbau) beiderseits der Bruchfläche bei einem Erdbeben). Die obere Hälfte der Lithosphäre verhält sich unter Einwirkung von Langzeit- oder säkularen Kräften wie ein elastischer Körper. In diesem Sinne kann man die Lithosphäre auch als elastisch beschreiben. Teile der Lithosphäre zeigen unter bestimmten Druck- und Temperaturbedingungen auch plastisches Verhalten. Dies zeigen geologische Strukturen wie Falten. Die obere hochviskose Gesteinseinheit der Lithosphäre weist eine stark temperaturabhängige Mächtigkeit auf. Die Untergrenze der elastischen Lithosphäre liegt bei einer Temperatur von etwa 600oC + 100oC (Turcotte, 1979). Daneben gibt es noch die Definition der thermischen Lithosphäre. Diese ist im ozeanischen Bereich um 50 bis 100 km mächtig, im kontinentalen Bereich im allgemeinen zwischen 100 bis 200 km (Meissner, 1986). Dabei liegt keine scharfe untere Grenze vor. Diese Grenze wird meist durch eine bestimmte Isotherme (thermische Lithosphäre) oder Viskosität definiert, die den Übergang zum duktilen Materialverhalten der Asthenosphäre anzeigt. Nach Turcotte (1979) liegt dieser Übergang bei einer Temperatur von 1200oC + 100oC vor. Im Gegensatz zur Lithosphäre können in der Asthenosphäre keine Bruchflächen unter Spannungsbedingungen entstehen. Die beliebige bleibende Verformung des Materials unter Stressbedingungen macht die Plastizität der Asthenosphäre aus.

Der noch zur Lithosphäre gehörende Mantel wird mit "Lid" bezeichnet (Panza et al., 1985). Die Unterscheidung zwischen Lithosphäre und Asthenosphäre erfolgt neben den oben genannten Merkmalen durch einen Kanal niederer Geschwindigkeiten seismischer Wellen, der im obersten Bereich der Asthenosphäre liegt. Die in diesem Kapitel zugrundegelegten Lithosphärenmächtigkeiten basieren auf der thermischen Definition der Lithosphäre, die Pollack und Chapman (1977) benutzten. Dazu haben die Autoren die Tiefe, in der sowohl die ozeanische als auch die kontinentale Geotherme 85 % der Schmelztemperatur erreichen, als Indikator für die Tiefe der Obergrenze der Zone niederer seismischer Geschwindigkeit identifiziert. Dies ist nach obigen Ausführungen gleich der Untergrenze des Lids, das oberhalb der Zone niederer Geschwindigkeit liegt. Pollack und Chapman (1977) setzen das Lid mit der Lithosphäre gleich und erhalten eine Weltkarte der Lithosphärendicke, die auf der regionalen Variation des Oberflächenwärmeflusses beruht.

Die Verletzbarkeit der Lithosphäre durch Intraplattenvulkanismus diskutierten Gass et al. (1978), Vogt (1981), Pollack et al. (1981), Summerfield (1983) und Pollack et al. (1983). Gass et al. (1978) definierten die dimensionslose Verletzbarkeit der Lithosphäre VL als

VL = µ / k d l = f (µ,l)

wobei k: thermische Diffusivität der Lithosphäre, d: charakteristische Entfernung zwischen sublithosphäri- schen, thermischen Störungen, l: Dicke der Lithosphäre nach Pollack und Chapman (1977), µ: Lithosphären (Platten-)geschwindigkeit, berechnet aus Rotationsvektoren von Minster und Jordan (1978).

Die Parameter k und d werden von Gass et al. (1978) sowie Pollack et al. (1983) als konstant angenommen, so daß die Verletzbarkeit der Lithosphäre nur von der Plattengeschwindigkeit und der Lithosphärendicke abhängt.

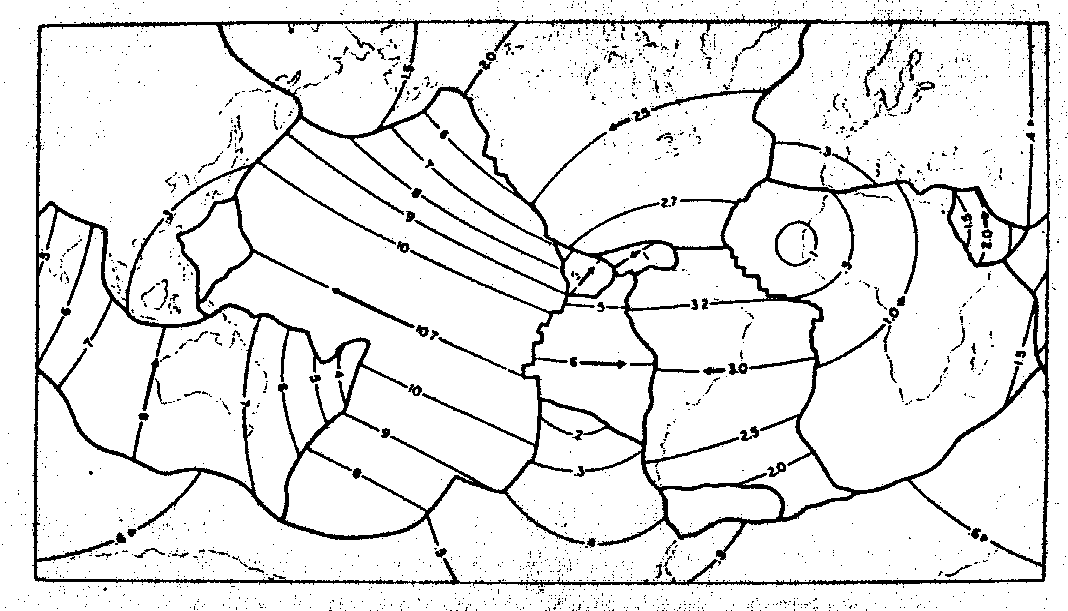
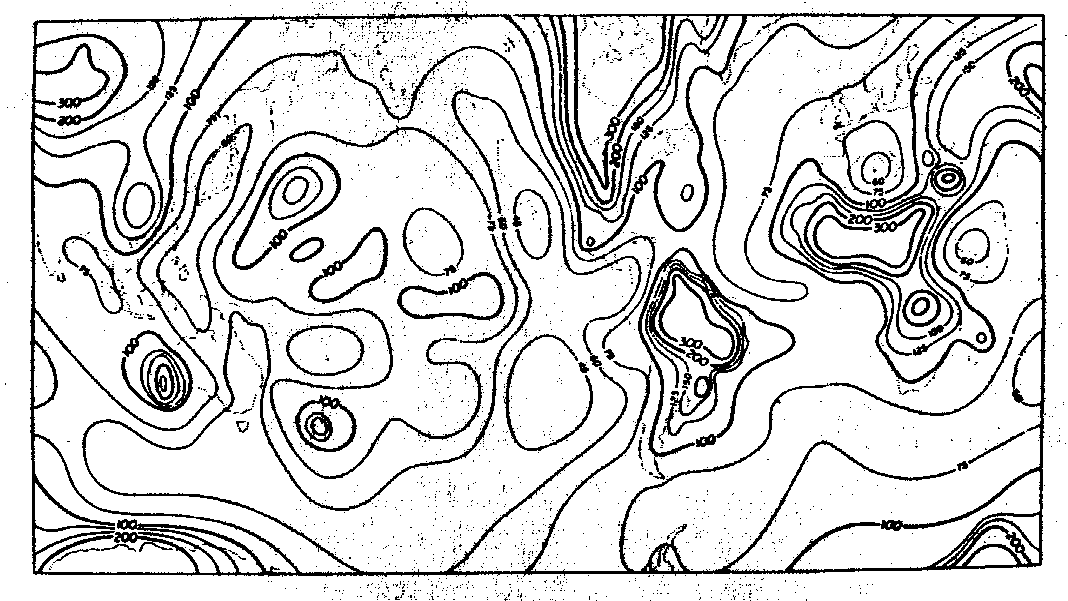
Die Plattendriftgeschwindigkeiten µ und die Lithosphärendicken l der Erde zeigt die Abb. 21. Je mächtiger die Lithosphäre, desto schwächer wird sich eine Wärmeanomalie der Sublithosphäre an der Oberfläche durchpausen. Je schneller sich die über der Wärmeanomalie liegende Platte bewegt, desto weniger wirksam kann sich die Wärme zur Oberfläche durchbrennen, da die Verweildauer eines Krustenteils über der Anomalie zu kurz ist. Danach sinkt also die Auftrittswahrscheinlichkeit von Hot Spots an der Oberfläche infolge von Mantel Plumes mit zunehmender Lithosphärendicke und zunehmender Plattengeschwindigkeit. Eine Korrelation der Lithosphärendicken und der Plattengeschwindigkeiten (Abb. 21) mit der Hot-Spot-Verbreitung (Abb. 17) besteht offenbar nicht. Der von Gass et al. (1978) definierte Parameter der Lithosphärenverletzbarkeit wird in Abb. 22 gezeigt. Die Hot-Spot-Verbreitung nach Abb. 17 korreliert jedoch kaum mit der von Gass et al. (1978) definierten Lithosphärenverletzbarkeit in Abb. 22. So lassen sich leicht sowohl Bereiche finden, in denen die Lithosphärenverletzbarkeit eine hohe Hot-Spot-Dichte erwarten läßt, die jedoch nicht vorliegt (z. B. Osteuropa), als auch Bereiche finden, in denen die Lithosphärenverletzbarkeit wenig Hot Spots erwarten läßt, wo aber sehr viele vorliegen (z. B. Afrika). Lediglich die Bereiche, die eine Lithosphärenverletzbarkeit VL > 10 aufweisen, sind erwartungsgemäß Hot-Spot-frei. Damit spiegelt die Superposition der Effekte aus Plattendrift und Lithosphärendicke auch nicht die Hot-Spot-Verbreitung wider. Folgende Ursachen kommen dafür in Frage: 1. Die Lithosphärenverletzbarkeit ist unzureichend definiert, 2. geologische Randbedingungen haben nicht zu vernachlässigende Einflüsse. Diese können sein: Zusammensetzung der Kruste und Petrologie, der Unterschied zwischen ozeanischer und kontinentaler Kruste, Krustenalter (steht in ozean. Regionen mit der Krustendicke im Zusammenhang), Vorliegen von Schwächezonen und lokale Anhäufung von Störungen, 3. Die Hot-Spot-Tätigkeit kann nicht allein als Funktion der physikalischen und chemischen Eigenschaften der Lithosphäre betrachtet werden.

Abb. 21. a. Plattengeschwindigkeiten in cm/Jahr nach Pollack et al. (1981), die nach Rotationsvektoren von Minster und Jordan (1978) berechnet worden sind;
b. Lithosphärenmächtigkeiten in km nach Pollack und Chapman (1977).

(1) und (2) hängen insofern zusammen, als daß die Verletzbarkeit der Lithosphäre von weiteren, nicht mittels einfachem Formalismus darstellbaren geologischen Parametern wie Störungen abhängt. Wäre die Hot-Spot-Verteilung ausschließlich als Funktion von Lithosphärenparametern darstellbar, würde dies weitreichende Konsequenzen haben: Entweder müßte eine statistische Verteilung der Mantel Plumes gefordert werden, so daß kein Gebiet ausgezeichnet ist, oder aber es müßte die Existenz der Mantel Plumes in Frage gestellt werden.

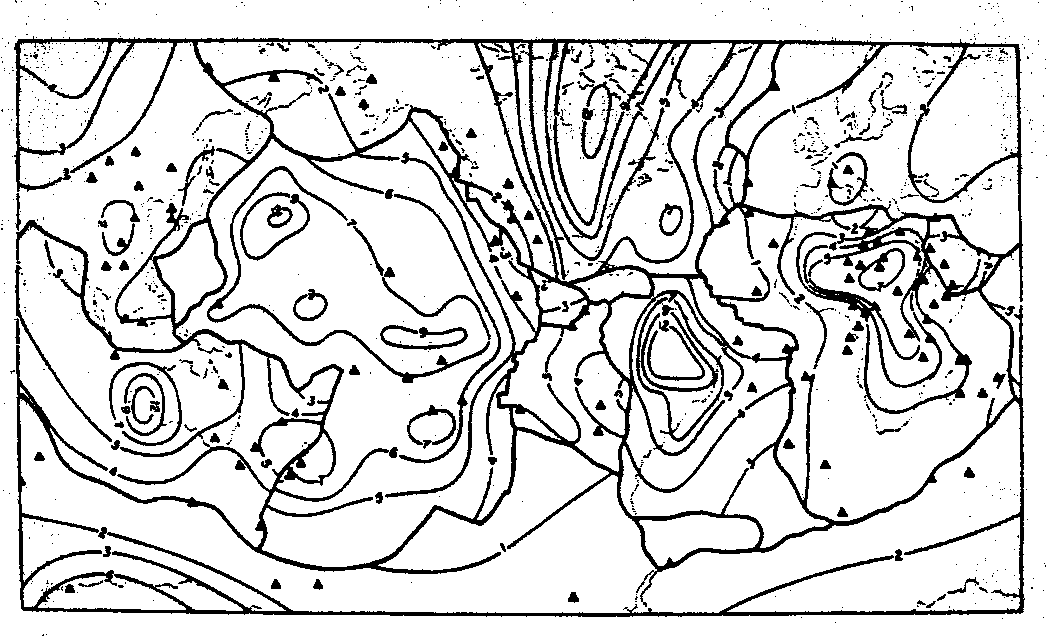
Abb. 22. Globalfeld des nach Gass et al. (1978) definierten Lithosphä- renverletzbarkeitsparameters VL. Die Hot Spots nach Pollack et al. (1983) sind durch die schwarzen Dreiecke markiert (Katalog 1). Kleine Werte charakterisieren eine hohe Verletzbarkeit und damit größere Wahrscheinlichkeiten für Hot Spots und vice ver- sa. Die dicken Linien markieren die Plattengrenzen.

Da insbesondere Letzteres sehr unwahrscheinlich ist, kann der Schluß gezogen werden, daß die Hot-Spot-Verteilung nicht allein als Funktion einer wie auch immer definierten Lithosphärenverletzbarkeit darstellbar ist. Diesen Aspekt greift (3) auf, wonach von den Eigenschaften der Lithosphäre unabhängige Ursachen die Verteilung der Hot Spots bestimmen bzw. im Falle einer teilweisen Abhängigkeit der Hot-Spot-Verteilung von der Struktur der Lithosphäre zumindest im entscheidenden Maße mitbestimmen.

Im Falle einer statistischen Verteilung der Mantel Plumes führen möglicherweise sowohl Konvektionsvorgänge sowie sonstige Zustände im Mantel als auch sehr komplexe, nicht beschreibbare Lithosphärenverletzbarkeiten dazu, daß dennoch keine Korrelation zwischen Lithosphärenverletzbarkeit und Hot-Spot-Verbreitung gefunden werden kann. Die in Kap. 4.2. abgeleitete nicht statistische Mantel-Plume-Hot-Spot-Verteilung spiegelt vermutlich das Auftreten von Mantel Plumes wider, so daß auch diese sehr wahrscheinlich nicht statistisch verteilt sind.

Nach Abb. 22 nimmt die dimensionslose Verletzbarkeit der Lithosphäre VL nach Gass et al. (1978) die Werte 0 < VL < 13 an. Es liegen einerseits z. B. die mittelatlantischen Hot Spots alle im Bereich niedriger Werte für VL und andererseits Hot Spots aufgrund hoher Plattengeschwindigkeiten (Pazifik) und hoher Lithosphärendicken (Afrika) in Bereichen mit relativ hohen VL-Werten um VL = 8. Somit lassen sich für Werte VL < 8 sowohl Gebiete mit als auch Gebiete ohne Hot Spots finden (vgl. Abb .22), so daß keine signifikante Korrelation der Hot-Spot-Verteilung (vgl. auch Abb. 17) mit der Lithosphärenverletzbarkeit nach Abb. 22 nachzuweisen ist. Daraus folgt für den Fall einer richtig angesetzten Definition der Lithosphärenverletzbarkeit die Existenz lithosphärenunabhängiger Ursachen für die Hot Spots.

Neben dem afrikanischen und pazifischen Raum, die beide mit relativ hohen Lithosphärenverletzbarkeitswerten (7 < VL < 8) ausgezeichnet sind und dennoch Hot Spots aufweisen, gibt es Gebiete mit Lithosphärenverletzbarkeiten um VL > 12. Es sind dies Ostnord- und Ostsüdamerika, der nordwestliche Pazifik sowie Westaustralien. Diese Gebiete weisen allesamt keine Hot Spots auf. Aus dieser Korrelation läßt sich der Schluß ziehen, daß die Struktur der Lithosphäre, hier die Mächtigkeit, einen Einfluß auf die Hot-Spot-Verbreitung hat.

Die Vorgänge in der Natur werden durch Wechselwirkungen bestimmt. Die für eine Wärmeanomalie undurchlässigere dicke Lithosphäre kann aber auch gerade die sublithosphärischen thermischen Anomalien durch den Effekt eines Wärmestaus hervorrufen. Auf diese Weise kann relativ zum Mantel unbewegte Kruste (z. B. Afrika) eine erhöhte Hot-Spot-Dichte infolge des Wärmestaus nach sich ziehen. Ferner ist es denkbar, daß es in Sublithosphärenbereichen, die unter Regionen schneller Plattendrift (vgl. Pazifik) liegen, zu einer labilen Temperaturschichtung und damit zu einer begünstigten Mantel-Plume-Bildung kommt, die sich ihrerseits an der Oberfläche durch vermehrtes Hot-Spot-Vorkommen zeigt.

Neben den bereits zitierten Autoren haben auch Marzocchi und Mulargia (1993) eine statistische Betrachtung der Verbreitung der Hot Spots durchgeführt. Dabei haben die Autoren folgende Parameter für die einzelnen Hot-Spot-Lokationen berücksichtigt: die Plattengeschwindigkeit, die minimale Entfernung zwischen benachbarten Hot Spots, die minimale Entfernung des Hot Spots zu einer Rückenachse und zu einer Subduktionszone, die Geoidanomalie (verschiedene Entwicklungen), die Fläche der Platte (auf welcher der Hot Spot liegt), die Mächtigkeit der Lithosphäre und der Stresszustand der Umgebung. Marzocchi und Mulargia (1993) finden, daß die Hot Spots durch im wesentlichen zwei Gruppen charakterisiert werden können: Zum einen liegen die Hot Spots in Bereichen positiver Geoidanomalien (bei einer Entwicklung von Grad 2 bis 10) und zum anderen liegen dicht beieinander liegende Vulkangruppen vor. Die Hot Spots der ersten Gruppe weisen oftmals Spuren (Vulkanketten) auf und liegen im Bereich der sich schnell bewegenden Platten. Die Hot Spots der zweiten Gruppe weisen einen Abstand von weniger als 900 km zu ihren Nachbarn auf und liegen im Bereich sich kaum bewegender Platten. Weiterhin sehen Marzocchi und Mulargia (1993) noch Ansätze für eine dritte Gruppe. Die Hot Spots dieser Gruppe liegen nahe bei den Rückenachsen. Die Ergebnisse von Marzocchi und Mulargia (1993) zeigen damit ebenfalls den in diesem Abschnitt beobachteten Trend (vgl. z. B. Kap. 3.2.3. und auch Abb. 17) und unterstützen die in Kapitel 4 gewonnenen Ergebnisse der Klassifizierung.

Die Korrelationen einzelner Parameter mit der Hot-Spot-Verteilung werden stets unzulänglich, da sie untereinander zusammenhängen. Die Lithosphäre kann als komplexer, mit dem Mantel wechselwirkender Filter angesehen werden. Diesen Filter kann man mittels seismischer Tomographie durchleuchten. Die Abb. 23 zeigt Ergebnisse tomographischer Untersuchungen.

3.3.3. Ergebnisse aus der seismischen Tomographie

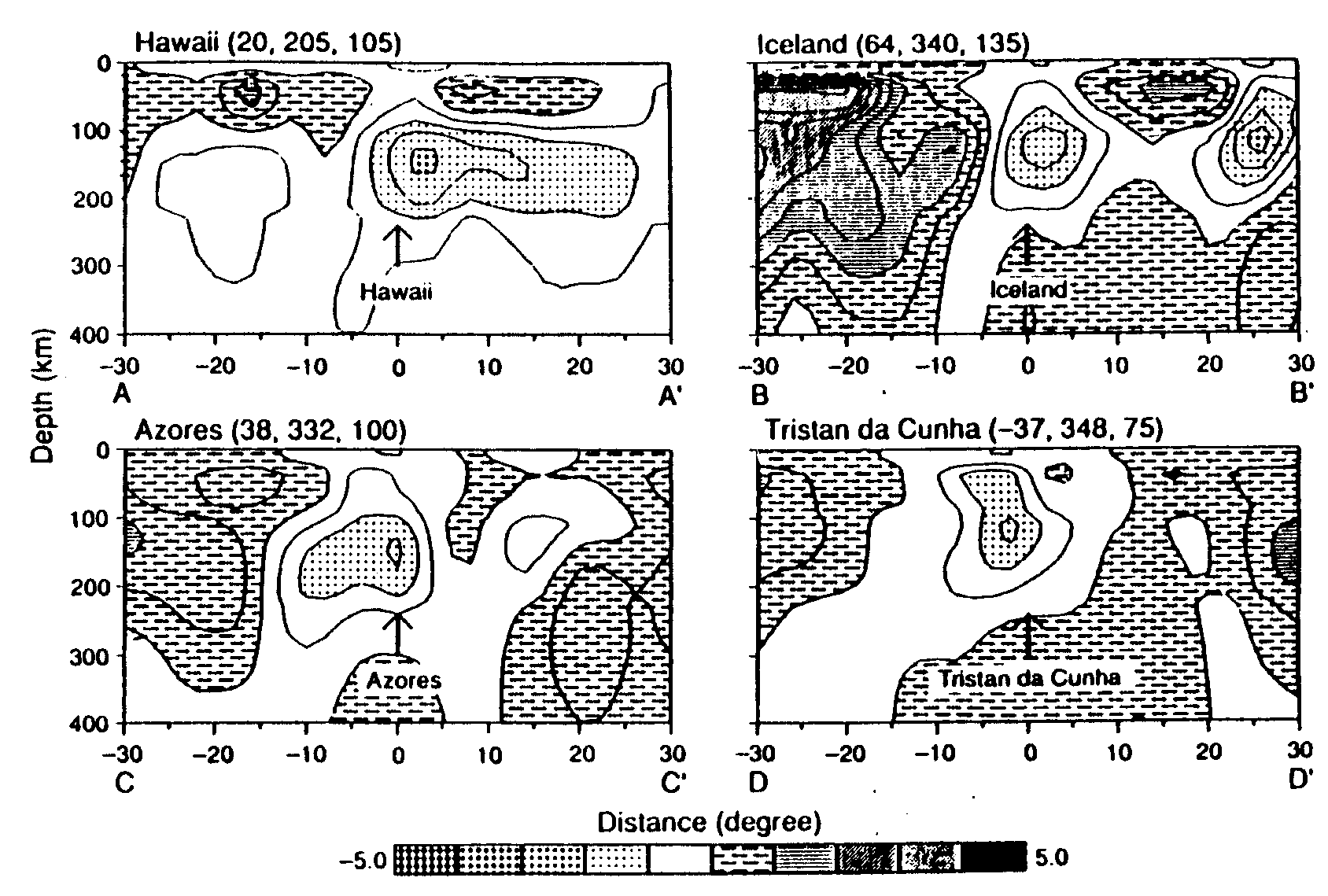
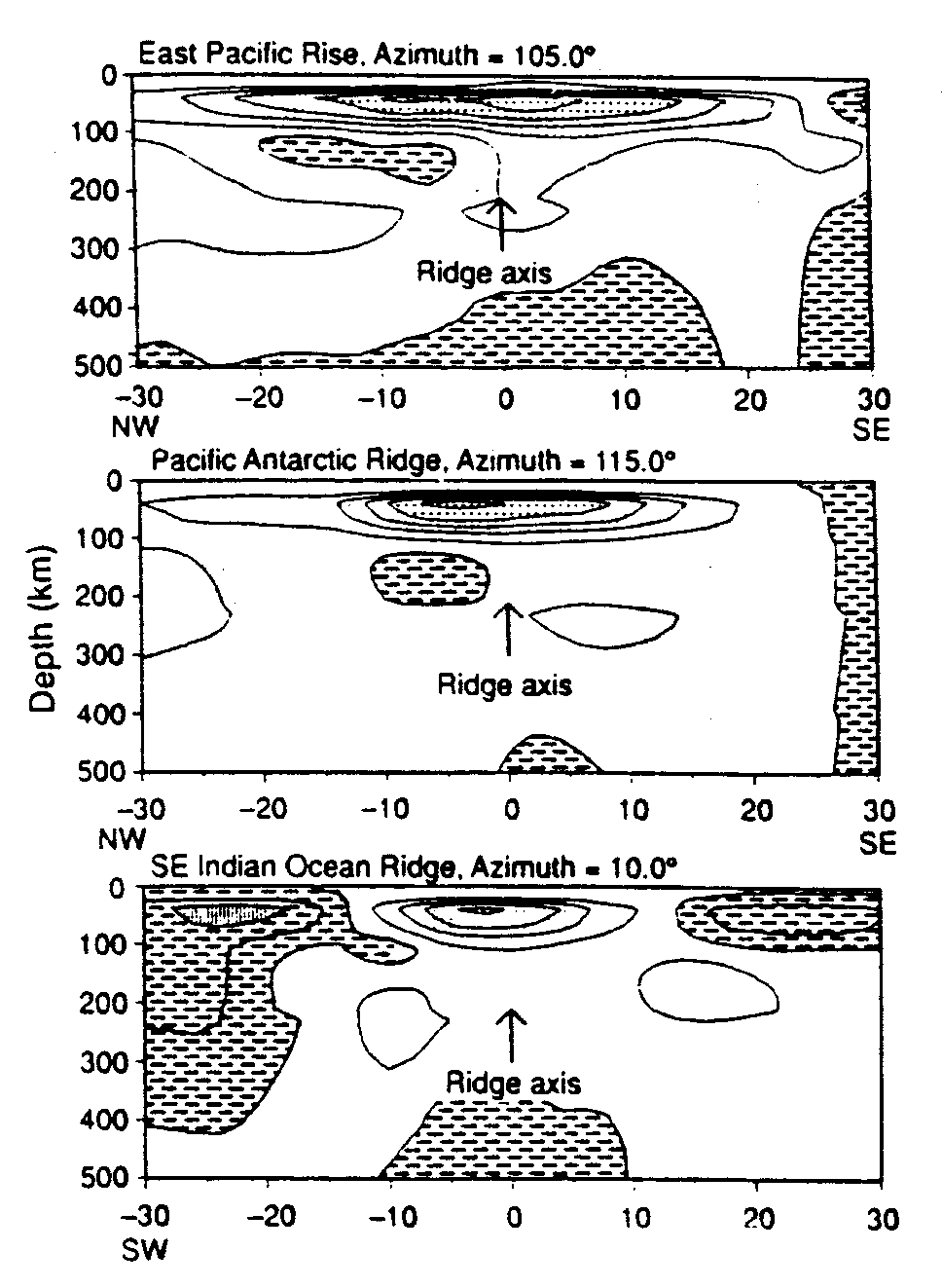
Abb. 23 stellt ausgewählte vertikale Profilschnitte der Geschwindigkeitsstruktur dar. Es zeigen sich die Geschwindigkeitsverteilungen für alle betrachteten Tiefen unter ausgewählten Hot Spots und Rückenachsen. Es ist klar zu sehen, daß Zonen erniedrigter Geschwindigkeiten in Tiefen um 60 km unter den Rückenachsen liegen. In diesen Bereichen liegen offenbar erhöhte Temperaturen vor. Bereits in 100 km Tiefe liegt dieses Signal nicht mehr vor. Damit zeigt sich, daß die Bereiche erhöhten Wärmeflusses im Falle der Rückenachsen nicht aus großen Tiefen kommen. Im Falle der Hot Spots zeigen sich die Anomalien der Geschwindigkeit nicht derart prägnant. Außerdem reichen die Geschwindigkeitsanomalien hier in wesentlich tiefere Bereiche hinab.

a) b)

c) d)

e)
f)
g)

Abb. 23. Tiefenschnitte für vier ausgewählte Hot Spots (a,b,c,d) und drei ozeanische Rückenabschnitte (e,f,g) nach Zhang und Tani- moto (1992). Die Geschwindigkeitsanomalien sind in Prozent des globalen Mittels der in der jeweiligen Tiefe vorliegenden Ge- schwindigkeit angegeben. a) Hawaii (20,205,105), b) Island (64, 340, 135), c) Azoren (38,332,100), d) Tristan da Cunha (-37,348,75); e) Ostpazifischer Rücken, f) Pazifisch-Antarktischer Rücken, g) Rücken d. südöstl. Indischen Ozeans. Die Zahlen in Klammern bedeuten die geographischen Koordinaten des Hot Spots und die Streichrichtung des Profils.

Eine Mantel-Plume-Struktur ist von erhöhter Temperatur. Das bedingt erniedrigte seismische Geschwindigkeiten. Die in Tiefen von 130 km beobachtbaren Bereiche erniedrigter seismischer Geschwindigkeiten weisen damit auf potentielle Mantel Plumes hin. Diese Tiefen entsprechen der für Mantel Plumes angenommenen sublithosphärischen Tiefenlage. Die Tomographie kann jedoch die schmalen Aufstiegskanäle der Mantel Plumes nicht auflösen.

Aus der Arbeit von Anderson et al. (1992) geht weiterhin hervor, daß unter der nordamerikanischen und der nordeurasiatischen Landmasse hohe Scherwellengeschwindigkeiten im oberen Mantel liegen. In diesen Gebieten gibt es weder nach Katalog 1 noch nach Katalog 2 Hot-Spot-Tätigkeit. In einer Tiefe von 60 km lassen sich offenbar plattentektonische Prozesse teilweise wiederfinden, da sich Rückenachsen in 60 km Tiefe meist durch verringerte Scherwellengeschwindigkeiten auszeichnen. Eine deutliche Korrelation zur Hot-Spot-Verteilung kann jedoch für keine betrachtete Tiefe festgestellt werden.

Aus der Arbeit von Anderson et al. (1992) kann ferner entnommen werden, daß einerseits nicht unter allen Hot Spots eine Zone verringerter Geschwindigkeit vorliegt und andererseits nicht jedem Gebiet verringerter Geschwindigkeit eine Hot-Spot-Lokation zugeschrieben werden kann. Der Rahmen auftretender Geschwindigkeitsanomalien verringert sich mit zunehmender Tiefe. Während in 60 km Tiefe Variationen zwischen -5 % und 5 % der globalen Durchschnittsgeschwindigkeit in der jeweiligen Tiefe vorkommen, liegt dieser Bereich in 490 km Tiefe nur noch bei -1 % bis 1 % (nach Anderson et al., 1992). Außerdem läßt sich aus den tomographischen Analysen ohne weiteres keine Aussage über global durchgreifende Konvektionssysteme ableiten.

Die sich in den folgenden Kapiteln weiterhin ergebenden Charakteristika für Mantel-Plume-Hot-Spots werden in Kap. 4.3.2.2. resumiert. Die Klassifizierung der Hot Spots in Kapitel 4 hat vorrangig zum Ziel, die Mantel-Plume-Hot-Spots von übrigen Klassen zu trennen. In Kapitel 4.2. wird dann die Verbreitung der Mantel-Plume-Hot-Spots, wie sie sich mit Hilfe der Ergebnisse aus Kapitel 3 ableiten läßt, vorgestellt.

zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite