zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite
8. Das dreidimensionale Dichtemodell des Mantel-Plume-Hot-Spots
Hawaii
8.1. Die Erarbeitung des Startmodells
8.1.1. Vorbereitende Überlegungen für das 3D-Modellieren
Da sich die zu modellierenden Strukturen sowohl parallel als auch senkrecht zur Hauptstreichrichtung in ihrer Form ändern, werden 3D-Modellrechnungen angewandt. Aus 2D-Modellrechnungen entlang ausgewählter Profile, die das zu untersuchende Gebiet in geeigneter Weise queren, lassen sich zwar ebenfalls Dichtemodelle ableiten, aber hierbei wird der Seiteneffekt von in benachbarten Profilen enthaltenen Strukturänderungen nicht erfaßt, da 2D-Berechnungen der Modellschwere auf einer unendlichen Ausdehnung des Modells quer zur Profilrichtung basieren. Im Falle sich kreuzender Profile kommt es überdies daher zu "cross-over-errors", d. h. an ein und derselben Raumkoordinate liegen zwei oder mehr verschiedene Modellschwerewerte vor. Auch im vorliegenden Falle wären 2D-Profile längs und quer zur Schwellenachse nicht ohne weiteres korrelierbar, da die Strukturen sich in beiden Richtungen rasch verändern und damit die beim 2D-Modellieren auftretende unendliche Ausdehnung nicht angenähert wird. Der nicht erfaßte Übergang zwischen benachbarten Profilen läßt sich durch ein 3D-Modell beschreiben. Neben Modellgeometrien in quer zur Schwellenachse angelegten Profilen lassen sich beim 3D-Modellieren Beginn und Ende längs der Schwellenachse auftretender Strukturen besser bestimmen.
Eine Änderung der Modellgeometrie in einem das 3D-Modell definierenden Profil verursacht bereits eine Veränderung der räumlichen Geometrie zwischen den benachbarten Profilen. Dadurch verändert sich das Schwerefeld des Modells auch im Bereich unverändert gebliebener Modellabschnitte. Ein Angleichen der Modellschwere an eine gemessene Schwere ist beim 3D-Modellieren aufwendiger als beim 2D-Modellieren. Eine gelungene Anpassung erhöht somit die Aussagekraft des 3D-Modells gegenüber einem aus einzelnen 2D-Profilen zusammengesetzten Modell (vgl. auch Kap. 9.1.).
Die Ergebnisse aus dem vorangegangenen Kapitel dienen nun zur Bestimmung eines Startmodells für die 3D-Dichtemodellierung von Hawaii. Diese wurde mit Hilfe des IGAS-Programmsystems (Götze, 1983; Götze und Lahmeyer, 1988) ausgeführt. Das 3D-Modell wird dabei aus 15 Profilschnitten zusammengesetzt, in denen die geologische Information steckt. Zur Berechnung des Schwerefeldes längs der Meereshöhe wird die Profilinformation mittels des Algorithmus nach Akima (1978) sowie Lawson (1972) zu einem 3D-Blockmodell interpoliert. Die Profile müssen parallel verlaufen, aber nicht in gleichem Abstand voneinander liegen. Eine optimal definierte Modellstruktur ergibt sich dann, wenn die Profile in Bereichen erhöhter Informationsdichte dichter zusammenliegen als in anderen Bereichen des zu betrachtenden Gebietes. Dies ermöglicht an wichtigen Stellen eine größere Detailbetrachtung. Außerdem bietet es sich an, die Profile senkrecht zum Streichen der wesentlichsten Strukturelemente zu legen.
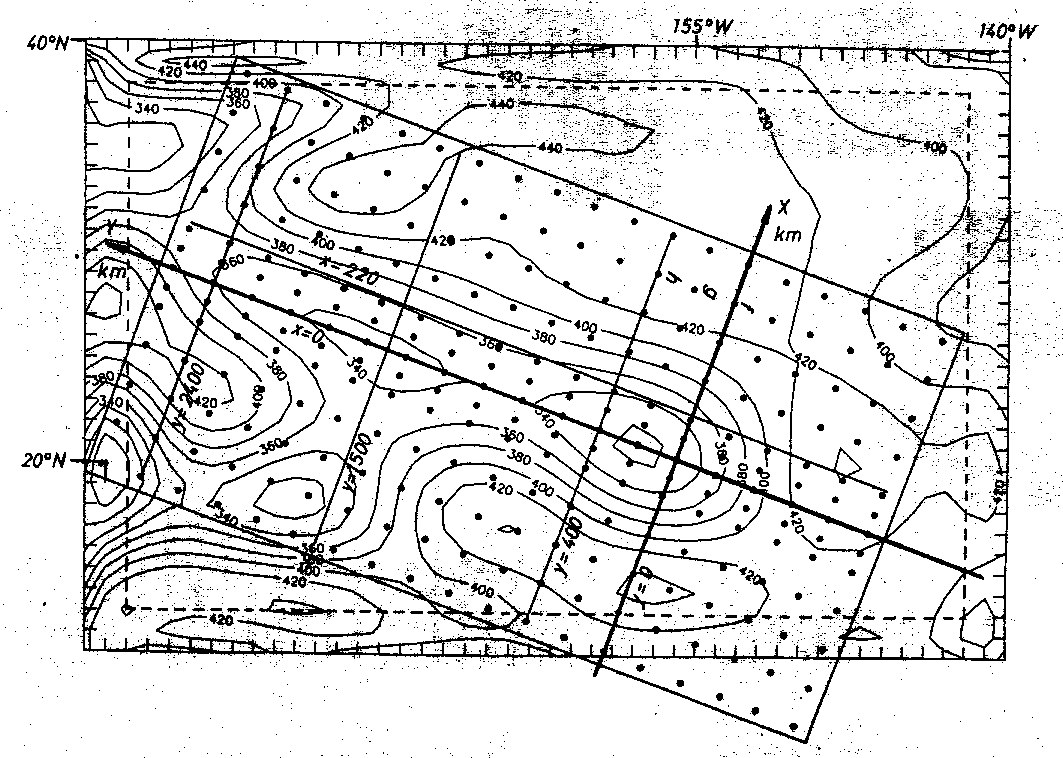
Das in Kapitel 6.1. in seiner geographischen Ausdehnung festgelegte Untersuchungsgebiet verjüngt sich polwärts. Da die Datengridpunkte in konstantem Abstand auf den Meridianen liegen, vergrößert sich polwärts damit die Datendichte in Ost-West-Richtung aufgrund des sich verringernden Meridianabstandes. Da die Hauptstreichrichtung der Hawaii-Inselkette etwa Ostsüdost-Westnordwest ist, bietet sich eine Streichrichtung für die Profile an, die etwa Nordnordost-Südsüdwest verläuft. Das Koordinatensystem im IGAS-Programmsystem ist kartesisch und in Kilometer geeicht. Daher wird es nötig, die aus gemessenen SEASAT-Daten berechneten langwelligen Bouguerschwere-Daten in ein entsprechendes System zu transformieren. Bei der Transformation werden die im geographischen Gradnetz in konstantem Abstand von 1 Grad vorliegenden Daten in Kilometer umgeeicht. Aufgrund der sich polwärts vermindernden Meridianabstände entspricht bei 20 Grad nördlicher Breite (Lage von Big Island) 1 Grad etwa 104,5 km, während dies am Äquator noch 111 km sind. Aufgrund der Ausdehnung des betrachteten Gebietes von etwa 10 bis 35 Grad nördlicher Breite liegt es nahe, im Mittel 1 Grad gleich 100 km zu setzen. Dies ergibt im Extremfalle eine Abweichung um 5 % vom wahren Wert. Der dadurch entstehende Fehler kann folglich vernachlässigt werden. Abb. 59 zeigt die Lage von 247 "Meßpunkten", an denen die Programmroutinen des IGAS-Systems die Modellschwere berechnen und diese mit der an diesen Punkten angegebenen Vergleichsschwere, der langwelligen Bouguerschwere, vergleichen.
Als Ursprung bietet sich die Lage von Big Island an. Die x-Richtung des IGAS-Programmsystems verläuft von Südsüdwest nach Nordnordost, also längs der Profile. Die y-Richtung verläuft parallel zur Inselkette von Hawaii von Westnordwest nach Ostsüdost. In diesen Achsen definiert liegt das Gebiet, für das das 3D-Modell erstellt werden soll, im Bereich
-2400 km < y < 1000 km sowie
-1000 km < x < 1000 km .
Damit liegt das Gebiet um Big Island bis zu einem Radius von 1000 km sowie die Umgebung der gesamten Hawaii-Inselkette westnordwestwärts im Modellbereich. Um den Randeffekt zu minimieren, wird das Modell über den obigen Rand hinaus in alle Richtungen bis in eine Entfernung von 36000 km extrapoliert. Damit können Fehlereinflüsse des Randes im eigentlichen Modellbereich vernachlässigt werden. Die Abstände zwischen den einzelnen das Modell definierenden Profilen sind um Big Island am geringsten, da hier das Zentrum der Mantel-Plume-Hot-Spot-Struktur angenommen wird.
Die exzentrische Lage des Zentrums im Modell verdeutlicht bereits, daß im folgenden Modellierprozeß nicht mehr von einem zylindersymmetrischen Mantel Plume (Abb. 42 und Abb. 43) ausgegangen wird, wie er in den allermeisten theoretischen Arbeiten dargestellt wird. Vielmehr wird hier aufgrund der Plattendrift von einer verzerrten Struktur ausgegangen, die bezüglich der Streichrichtung der Inseln zwar noch achsensymmetrisch, aber nicht mehr zentralsymmetrisch angelegt ist.
Ziel der Arbeit ist es, ein Mantel-Plume-Hot-Spot-Dichtemodell zu schaffen, das die langwelligen Anteile der Bouguerschwere wiedergibt. Abb. 52 zeigt die als mögliche Vergleichsschwere dienenden Schwerefelder. Sie unterscheiden sich im Grad der Tschebyschev-Anpassung an die Originaldaten (Abb. 46). Im Falle des 6. Grades kommt die Hawaii-Schwelle nur unzulänglich heraus. Die Vereinfachung ist zu stark. Für Grad 10 hingegen zeichnen sich erste lokalere Strukturen ab, die ebenfalls nicht modelliert werden sollen. Als eine geeignete Darstellung kommt die Anpassung vom Grad 9 in Frage. Hier ist die regionale Bougueranomalie um Big Island mit entsprechender Verlängerung in Richtung der Hawaii-Inselkette am besten abgebildet worden. Damit gehen die Daten nach Abb. 52d als Vergleichsschwere in das Programmsystem IGAS ein und stehen als konstanter Parameter für das Anpassen der Modellschwere durch alle Modellierungen zum Vergleich zur Verfügung.

Abb. 59.
Lage der "Meßpunkte", an denen die Daten der Bouguerschwerekar-
te nach Abb. 52d im Programmsystem IGAS vorliegen und die Mo-
dellschwere berechnet wird (schwarze Punkte). Die Abbildung
zeigt das Koordinatensystem, über welches 2D-Profile aus dem
3D-Modell angesprochen werden. Die x-Achse verläuft in nord-
nordöstlicher und die y-Achse in westnordwestlicher Richtung.
Profile senkrecht zum Streichen der Schwelle sind durch kon-
stante y-Werte und Profile parallel zur Schwellenachse durch
konstante x-Werte gekennzeichnet. Für die 2D-Darstellung des
3D-Modells werden in diesem Kapitel mehrfach die eingetragenen
Profillagen diskutiert. Die gestrichelte Linie gibt den Bereich
an, in dem die Daten der Bouguerschwere Randeffekte enthalten
können (vgl. Kap. 6.3.). Der Ursprung des Koordinatensystems
liegt über dem Hot-Spot-Zentrum (Big Island, Insel Hawaii).
Die Lage der Profile, entlang derer die 3D-Modellgeometrie de-
finiert wird, zeigt u. a. Abb. 71.
Die Darstellung des regionalen Schwerefeldes hat empirische Züge und hätte nicht nur mit der Wahl eines anderen Approximationsgrades (vgl. Abb. 52 in Kap. 6.3.), sondern auch durch andere Filtermethoden anders ausfallen können. Daher ist es nicht zwingend notwendig, die Anpassung der Modellschwere an die Vergleichsschwere, die rechnerisch aus Meßdaten gewonnen worden ist, auf z. B. 1 mGal genau anzustreben. Dadurch wird keinerlei verbesserte Aussagekraft über die Problematik, im Rahmen dieser Arbeit eine bessere Evidenz für die Existenz hypothetischer Strukturen zu finden, gewonnen, zumal nach Abb. 44 eine unendliche Zahl von Lösungen für eine Schwerekurve möglich sind. Die Anpassung wird im Rahmen der durch die verschiedenen mathematischen Beschreibungsmöglichkeiten der Bouguerschwere, die auf lokale Abweichungen bis etwa 10 mGal hinauslaufen, auf eine dementsprechende Genauigkeit angestrebt. Da hier geprüft wird, ob die Schwere- und Geoiddaten überhaupt und inwieweit mit den hypothetischen Modellen vereinbar sind, ist lediglich eine Modellierung von Strukturen nötig, die im Rahmen der Anpassung der Modellschwere an die Vergleichsschwere die Form, Amplitude und Wellenlänge des Schwerefeldes der Schwelle wiedergibt. Diese fundamentalen regionalcharakteristischen Eigenschaften wären auch durch andere Grade einer Tschebyschev-Approximation oder gar einer anderen Filtermethode nicht wesentlich verändert worden.
8.1.2. Die 3D-Modellidee
Die Profile im Bereich des Zentrums (Ursprung) werden im wesentlichen durch die Dichten und Geometrien, die Kapitel 7 herausgestellt hat, bestimmt. Abb. 60 zeigt eine Idee für ein Startmodell, wie sich die Ergebnisse aus Kapitel 7 längs der Streichrichtung der Hawaii-Kette verändern könnten. Dies läßt sich mit Hilfe des 3D-Modellierens erfassen.
Die Idee dieses Modells basiert auf den folgenden Überlegungen. Ziel des Modellierens muß es sein, möglichst die Bougueranomalie nach Abb. 52 zu erhalten. Hier wird der Modellbereich durch ein "ellipsenförmiges" Bouguertief charakterisiert, in dessen Zentrum sich die Hawaii-Kette befindet. Da sich das geographische Zentrum dieses Bouguertiefs nicht unter Big Island oder Loihi Seamount, wo das Zentrum des hypothetischen Mantel Plumes angenommen werden soll, liegt, kann das Bouguertief nicht allein auf eine Mantel-Plume-Struktur zurückführbar sein. Im Falle eines zylindersymmetrischen Mantel Plumes (gepunktete Linie in Abb. 60b) um Big Island müßte sich ein um Big Island konzentrisch ausgebildetes Tief abzeichnen, falls weitere Störeinflüsse nicht vorliegen würden. Liegt mit Störeinflüssen aber dennoch unter Big Island eine zylindersymmetrische Mantel-Plume-Struktur, so müssen diese Störeinflüsse westnordwestwärts stark an Dominanz dergestalt zunehmen, daß es zur Ausbildung der ellipsenförmigen Bougueranomalie kommen kann. Dies ist eher unwahrscheinlich.
Denkbar wäre jedoch eine Mantel-Plume-Struktur, die durch Superpostion mit der Konvektionsströmung (Pfeil in Abb. 60) hinsichtlich der Plattendrift westnordwestwärts verzerrt ist. Bliebe das Zentrum eines solchen Mantel Plumes aber dennoch unter Big Island, so würde sich eine "eiförmige", nach Westen sich verjüngende Bougueranomalie zeigen. Da auch dies nicht der Fall ist, könnte man zusätzlich annehmen, daß es zu einer Plume-Lithosphären-Wechselwirkung gemäß der in Kapitel 7 beschriebenen und in Abb. 58 dargestellten Superposition der Schwellenursachen nach Abb. 54c,d,e kommt, wobei westnordwestwärts die Mächtigkeit der alterierten Lithosphäre (Kap. 7.1.2.) zunächst noch zunimmt.
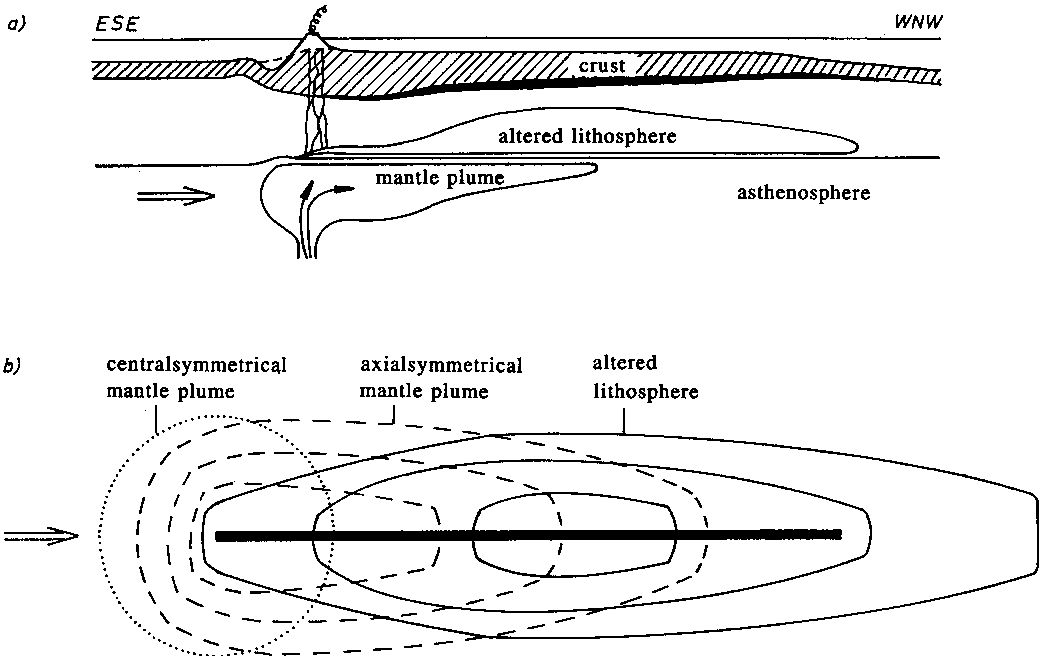
Abb. 60.
Startmodellidee zur dreidimensionalen Modellstruktur des ha-
waiianischen Mantel-Plume-Hot-Spot-Systems, dargestellt als
a) Seitenansicht in Streichrichtung längs der Schwellenachse
und
b) als transparente Aufsicht.
a) stellt das Profil entlang der Schwellenachse dar. Direkt
über dem Aufstiegszentrum des Mantel Plumes kommt es zu Vul-
kanismus, während sich der Plume selbst durch Strömungen
verformt. Aufgrund der Relativbewegung zwischen Lithosphäre
und Asthenosphäre kommt es zu einer alterierten Lithosphäre,
die ihr Maximum erst nach dem Passieren des Plumezentrums
erreicht. Die Kruste ist im Schwellenbereich unter der Vul-
kanauflast verdickt. Der dicke schwarze Strich unterhalb der
Kruste soll den möglichen subkrustalen Intrusivkörper nach
Abb. 38 andeuten.
b) zeigt die Lage eines zentral- oder zylindersymmetrischen
Plumes (gepunkteter Kreis), der unter dem Einfluß einer
Strömung axialsymmetrisch zur Schwellenachse deformiert wird
(gestrichelte Linien). Die verzögert auftretende alterierte
Lithosphäre ist durch die durchgezogenen Linien dargestellt.
Die verschiedenen ineinander liegenden Linien geben die Zu-
nahme der Mächtigkeit zum Zentrum der jeweiligen Struktur
an. Der dicke schwarze Balken markiert die Zone des zentra-
len Hot-Spot-Inselketten-Vulkanismus.
Für die Zunahme der Mächtigkeit eines Bereiches alterierter Lithosphäre westnordwestlich des Hot Spots spricht z. B. auch ein thermisches Modell, das Sleep (1978b) berechnete. Darin wird ein "lithospheric heating" westnordwestlich der Insel Hawaii, dem Zentrum des Hot Spots, vorgeschlagen. Für dieses Modell sprechen auch Wärmeflußmessungen, die von Herzen et al. (1982) und von Herzen et al. (1989) vorgenommen haben. Zwar stellen die Autoren ihre Wärmeflußwerte aus von Herzen et al. (1982) z. T. in Frage, kommen aber in von Herzen et al. (1989) zu dem Schluß, daß, wenn eine Wärmeflußanomalie über der Hawaii-Schwelle vorliegt, diese dann ihr Maximum westnordwestlich der Hawaii-Inseln bei den Midway-Inseln erreicht.
Danach ist es möglich, daß eine ausgedehnte Aufheizung der Lithosphäre in dem Bereich, der bereits das Zentrum des Mantel Plumes passiert hat, stattfindet. In diesem Sinne erfolgen die durchgreifendsten, räumlich ausgedehntesten Veränderungen in der Lithosphäre erst nach längerer Einwirkung des Plumekopfes auf die Lithosphäre. Dies zeigt, daß der Prozeß der Alteration der Lithosphäre nicht mit dem Auftreten des Vulkanismus zum Erliegen kommt, sondern vielmehr zeitgleich weiter voranschreitet. Durch die Bewegung der pazifischen Platte jedoch liegen die Zone des zentralen Auftreffens des Plumes (wo sich der Vulkanismus zeigt) auf die Lithosphäre und der Bereich der extensivsten Plume-Lithosphären-Wechselwirkung nicht übereinander, sondern versetzt. Eine solche Kombination der Effekte von Mantel-Plume-Lithosphären-Wechselwirkung beinhaltet die Abb. 60. Dies stellt somit eine zeitliche und räumliche Trennung der in Kap. 7.1.1. beschriebenen Superposition kausal zusammenhängender Modelle dar. Ferner weist dies auch auf die mögliche Deformation des Plumes hin.
In der Asthenosphäre findet die Wärmeübertragung im wesentlichen durch den Plume und damit durch Konvektionsprozesse statt. In der Lithosphäre hingegen dominiert insbesondere die Wärmeleitung. Der in Abb. 60 angedeutete subkrustale Intrusivkörper (vgl. Abb. 38) liegt nur im Bereich der Vulkankette. Aufgrund der geringen Ausdehnung bleibt diese Struktur bei Hawaii nur von lokaler Bedeutung und kann bei der Modellierung der regional wirksamen Ursachen zur Schwellenbildung nicht aufgelöst werden. Der Vergleich von Abb. 38 und Abb. 39 zeigt überdies, daß der subkrustale Intrusivkörper bei Hawaii mittels gravimetrischer Methoden nicht nachgewiesen werden kann: Die gemessene Schwere läßt sich durch eine Flexur der Kruste sowohl mit als auch ohne einem subkrustalen Intrusivkörper darstellen. Daher kann, obwohl die seismischen Ergebnisse nach Abb. 37c auch in Verbindung mit Meissner und Köpnick (1988) für einen subkrustalen Intrusivkörper sprechen, als Vereinfachung eine gemäß Abb. 39 definierte Krusten-Mantel-Grenze (vgl. Abb. 61t und Abb. 72t im ANHANG) in der 3D-Modellentwicklung angesetzt werden, die auch in Verbindung mit einem subkrustalen Intrusivkörper interpretierbar ist. Hierdurch wird weder die Existenz eines subkrustalen Intrusivkörpers noch die Aussagekraft der 3D-Modelle in Frage gestellt.
In Kap. 5.4. und Abb. 40 wird der sublithosphärische Plumekopf zylindersymmetrisch dargestellt. Aufgrund der Bewegung der pazifischen Platte von Westsüdwest nach Ostnordost wird die Form des Plumekopfes, der bei einer unbewegten Platte zylindersymmetrisch wäre, verzerrt. Er wird gegen die Bewegungsrichtung ("stromaufwärts") gestaucht und mit der Bewegungsrichtung ("stromabwärts") gedehnt (vgl. Abb. 60b). Dieser Vorgang läßt sich durch eine sogenannte "stagnation streamline" (Sleep, 1987b; Olson, 1990) beschreiben. Die "stagnation streamline" definiert die Stelle, an der heißes Plume-Material mit dem kühleren asthenosphärischen Material in Kontakt tritt. In diesem Sinne ist die "stagnation layer" die Oberflächengeometrie des Plumekopfes. Die Form der "stagnation streamline" nach dem "refracted plume"-Modell von Olson (1990) wird qualitativ übernommen. Die genaue Oberflächengeometrie des Modellplumes wird sich dann aus der Anpassung an die Vergleichsschwere ergeben (vgl. Kap. 8.4.).
8.1.3. Das Startmodell
Abb. 61 (siehe auch im ANHANG) zeigt die Struktur des Startmodells, wie es in den zur Verfügung stehenden 15 Profilen empirisch aus den vorangegangenen Ergebnissen definiert worden ist. Dieses Startmodell repräsentiert nicht die Diskussionsgrundlage für die Mantel-Plume-Hot-Spot-Struktur, diese soll ausgehend von diesem Ansatz im Rahmen dieser Arbeit erst noch als Abschlußmodell durch Anpassung der Modellschwere an die Vergleichsschwere erarbeitet werden. Die Ergebnisse für die Modellschwere in
Abb. 61. (nachfolgend)
Das 3D-Startmodell für den Mantel-Plume-Hot-Spot von Hawaii,
definiert in 15 Profilschnitten. Die Darstellungen von a) bis
q) geben die Struktur der alterierten Lithosphäre und des
Plumes an, die Darstellungen r) bis v) die Geometrie der Kru-
sten-Mantel-Grenze. Die Modellschwere ist über jedem Profil ge-
strichelt, die Vergleichsschwere durchgezogen eingetragen. Die
Lage der Profile ist über die y-Koordinate gemäß Abb. 59 defi-
niert. Folgende Modelldichten wurden verwendet:
Kruste: 2,95 g/cm
f) Querprofil bei y = 0 (Hot-Spot-Zentrum).
h) Querprofil bei y = 400 km (etwa Lage des Profils aus Kap. 5).
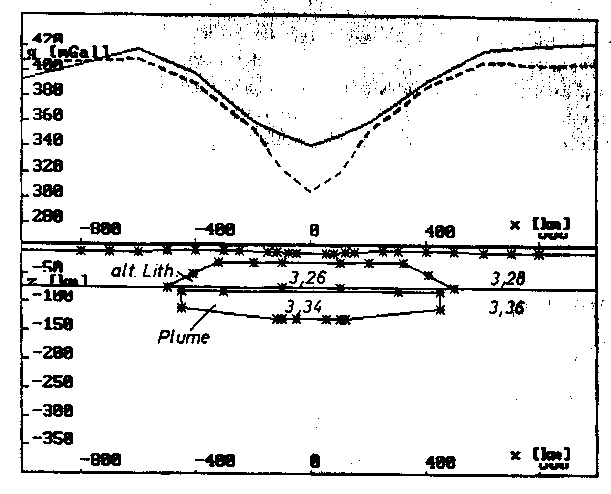
k) Querprofil bei y = 1000 km.
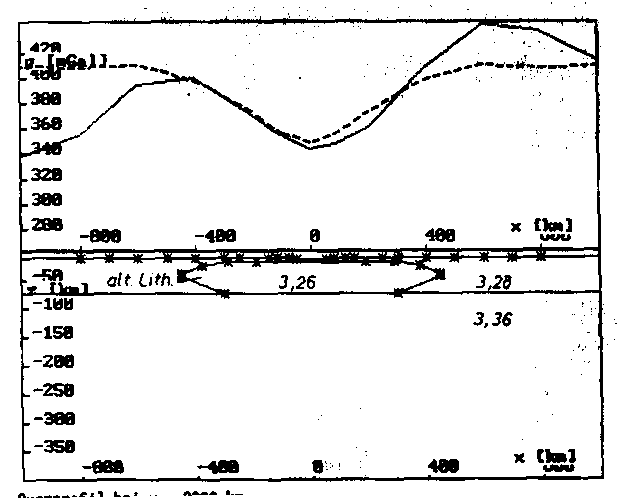
n) Querprofil bei y = 2000 km.
Abb. 61 geben einen ersten Hinweis auf die Effekte der 3D-Modellierung. Zum besseren Verständnis der 3D-Struktur des Modells zeigt Abb. 62 den Aufbau des Startmodells längs mehrerer Profile parallel zur Hauptstreichrichtung der Hawaii-Schwelle, der Schwellenachse. Hier kommt der Vergleich mit der Idee nach Abb. 60 gut heraus.
Das Startmodell enthält folgende geologische Strukturen mit ihren Dich-
ten: a. Kruste mit der Dichte 2,95 g/cm3 (Dabei ist der Wasserkör-
per bei der Berechnung der Bouguerschwere als Vergleichs-
schwere mit einer Reduktionsdichte von 1,95 g/cm3 aus den
Freiluftdaten in Kap. 6 weggerechnet worden. Die Dichte von
2,95 g/cm3 stellt einen Mittelwert für die gesamte Krusten-
struktur dar.
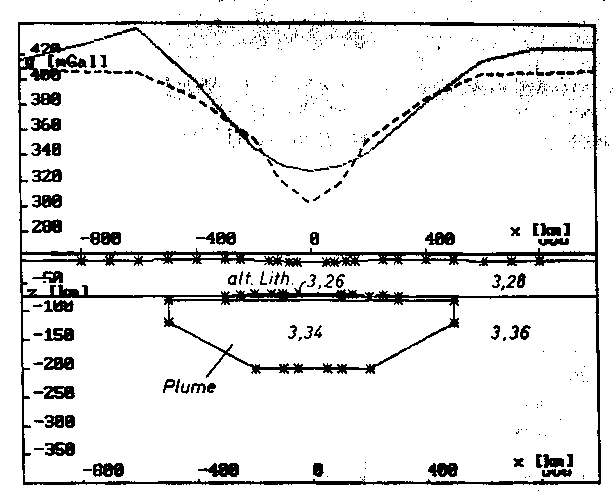
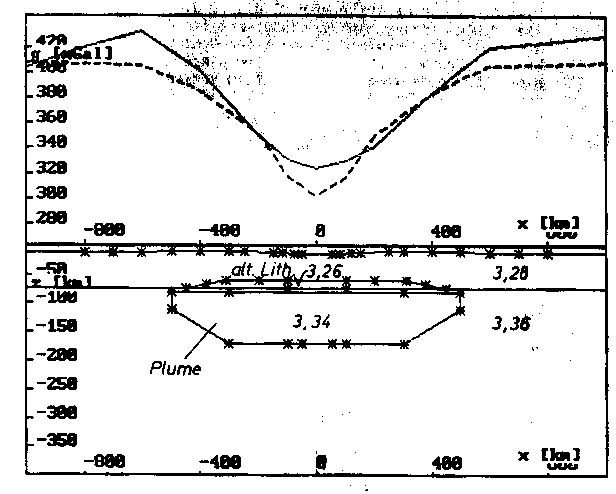
Abb. 62. (nachfolgend) Der Aufbau des Startmodells, gesehen in Profilen parallel zur
Hauptstreichrichtung der Modellstruktur. Es gelten die Dichten
für die Geometrien nach Abb. 61. Die Modellschwere ist gestri-
chelt und die Vergleichsschwere durchgezogen eingetragen.
a) Profil der Schwellenachse x = 0,
b) x = 220 km,
c) x = 400 km.
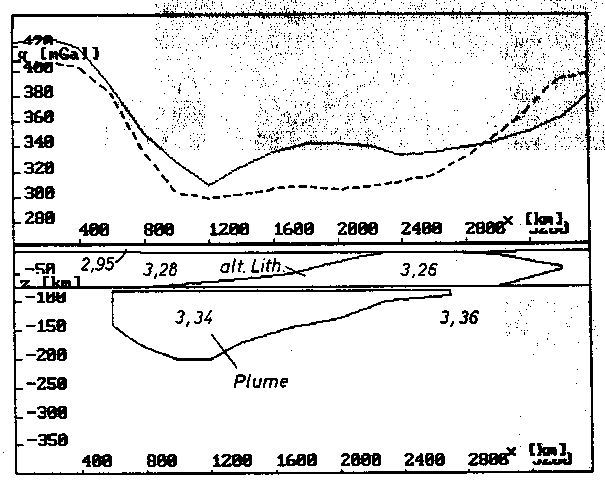
a) Längsprofil x = 0 (Schwellenachse).
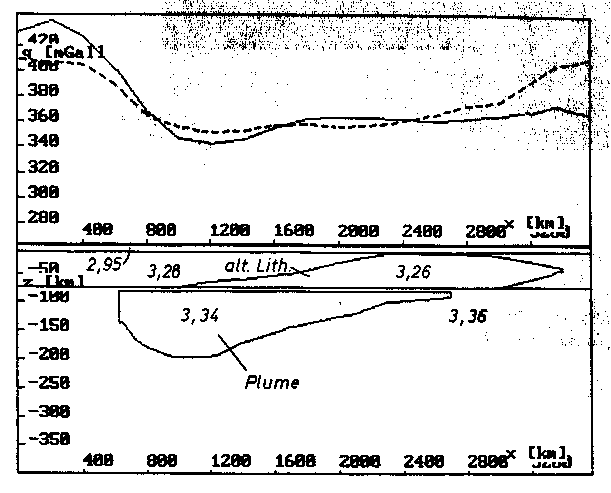
b) Längsprofil x = 220 km.
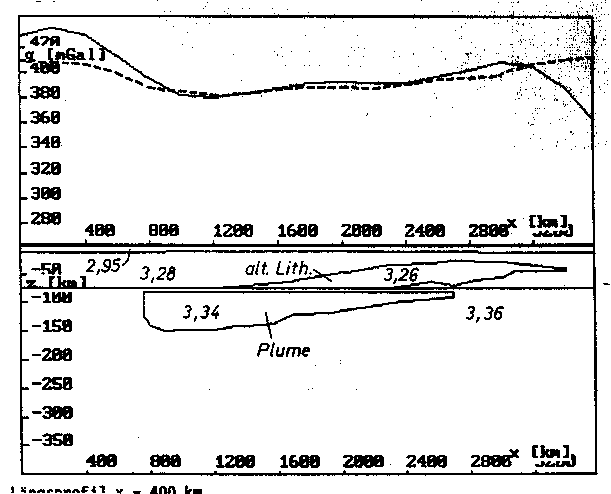
c) Längsprofil x = 400 km.
b. Lithosphäre mit der Dichte 3,28 g/cm3,
c. alterierte Lithosphäre mit der Dichte 3,26 g/cm3,
d. Asthenosphäre mit der Dichte 3,36 g/cm3,
e. Mantel Plume mit der Dichte 3,34 g/cm3.
Die Abb. 63, Abb. 64 und Abb. 65 zeigen in Form einer Karte der Modellschwere des Untersuchungsgebietes die einzelnen Beiträge der beteiligten Strukturen. Nicht berücksichtigt ist hierbei die Grenze zwischen Lithosphäre und Asthenosphäre. Sie ist lediglich über dem zentralen Plume-Bereich angedeutet. Ihr Beitrag zur Schwere verschwindet gegenüber der Plume-Struktur nahezu (siehe Abb. 56). Die genaue Struktur dieser Grenze wird bei der Diskussion im Rahmen der Verfeinerung des Startmodells zum Abschlußmodell mit einbezogen.
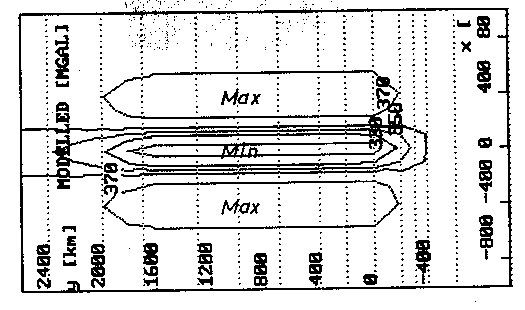
Abb. 63. Das 3D-Startmodell; Beitrag der Krusten-Mantel-Grenze mit einem
Dichtekontrast von 0,33 g/cm
Das Schweresignal der Krusten-Mantel-Grenze zeigt ein langgestrecktes zentrales Minimum und beiderseits der Längsachse dieses Minimums Randmaxima. Im Vergleich mit Abb. 55, welche die Schwere für ein Profil quer zur Längsachse des Minimums zeigt, erklärt sich das Minimum durch die Kompensation der Vulkanmassive. Die Wurzel taucht in den Mantel ein. Die Randmaxima gehören zu der Schwelle. Danach ist dort die Kruste hochgebogen. Dies geschieht nach Abb. 54 durch unterschiedliche Ursachen, die bereits in Kap. 7.1.1. erläutert worden sind. Diese Zusammenhänge werden auch anhand von Abb. 69 in Kap. 8.3. deutlich. Hier zeigen die mit "+"
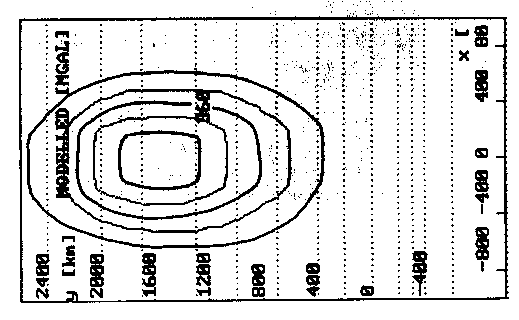
Abb. 64. Das 3D-Startmodell; Beitrag des Bereichs alterierter Lithosphä-
re, angesetzt mit einer um 0,02 g/cm
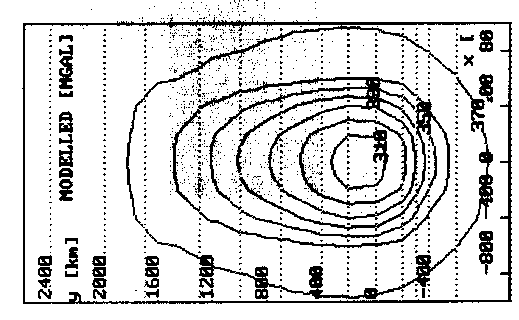
Abb. 65. Das 3D-Startmodell; Beitrag des Mantel Plumes mit einer gegen-
über der Asthenosphäre um 0,02 g/cm
gekennzeichneten Gebiete Massenüberschüsse an, die dann zu den Randmaxima beitragen. Die hochgebogene Kruste verursacht einen Massenüberschuß (vgl. dazu auch Abb. 69) durch das bei einer konstanten Mächtigkeit der Kruste in den Bereich unterhalb derselben eingedrungene, dichtere Material der Lithosphäre. Die Minima in den Abb. 64 und Abb. 65 erklären sich durch die defizitären Massenanomalien der modellierten Strukturen.
8.1.4. Vergleich der Startmodellschwere mit der aus gemessenen
Werten berechneten langwelligen Schwere
Die genaue Defintion des 3D-Startmodells ist dargestellt durch Abb. 61. Dabei wird zu jedem Profil die aus gemessenen Werten berechnete langwellige Bouguerschwere im Vergleich zur Modellschwere angezeigt. Der 3D-Gesamtzusammenhang tritt in dieser Darstellung eher in den Hintergrund. Daher ermöglicht das Programmsystem IGAS die Darstellung der Daten auch in Form eines zweidimensionalen Feldes, eines Isolinienplanes. Die Abb. 66 zeigt die Modellschwere.
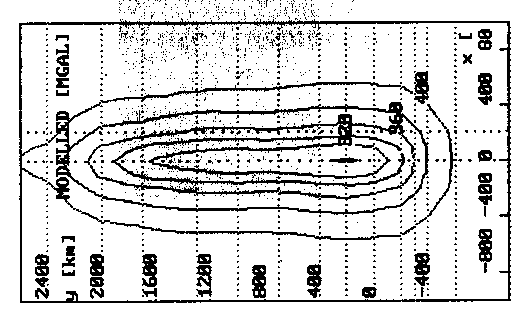
Abb. 66. Das Modellschwerefeld des Startmodells. Die gepunkteten Linien
konstanter y-Werte markieren die Lage der modelldefinierenden
Profile nach Abb. 61. Der Abstand zwischen den Isolinien be-
trägt 20 mGal.
Es ergibt sich eine recht gute Übereinstimmung der Amplituden und Wellenlängen der Startmodellschwere (Abb. 66) mit der berechneten Bouguerschwere im Bereich der Schwelle (Abb. 52d, Abb. 59 oder Abb. 71). In beiden Darstellungen wird die Schwelle in erster Näherung durch die 400mGal-Isolinie markiert. Bei genauerem Hinsehen erkennt man jedoch einige Abweichungen. Die prägnantesten beziehen sich auf Strukturen im Umgebungsbereich der Schwelle, die im Modell nicht enthalten sein sollen und können. In diesen Bereichen wird es zu keiner sinnvollen Anpassung der Modellschwere zur Bouguerschwere kommen, da über diese Strukturen kaum etwas bekannt ist und ferner sich das Modellieren auf die Hawaii-Schwelle konzentrieren soll.
Von Bedeutung sind somit nur die Abweichungen, die die Schwelle direkt betreffen. Abb. 67 zeigt die Residuen zwischen Bouguer- und Modellschwere. Positive Differenzen bedeuten, daß die Vergleichsschwere (regionale Bouguerschwere) größer als die Modellschwere ist (Modellschwere zu niedrig). Bei negativen Differenzen ist die Modellschwere zu hoch. Die schwellenunabhängigen Ursachen treten insbesondere im Südwesten des Untersuchungsgebietes auf. Im Bereich der Schwelle zeigen sich im Zentrum positive Abweichungen um etwa 20 mGal, in den Randbereichen liegen die Abweichungen bei etwa -10 mGal.
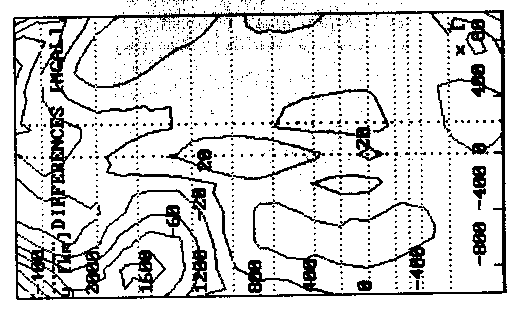
Abb. 67. Differenzfeld aus Startmodellschwere und berechneter, aus ge-
messenen Daten abgeleiteter Bouguerschwere. Positive Differen-
zen liegen bei zu kleiner und negative Differenzen bei zu gro-
ßer Modellschwere vor. Der Abstand zwischen den Isolinien be-
trägt 20 mGal.
Ferner zeichnet sich in der Vergleichsschwere (vgl. Abb. 71) neben dem Bouguerminimum im vorderen Schwellenbereich über der Hot-Spot-Lokation ein weiteres Nebenminimum im hinteren Bereich der Schwelle ab. Dies wird vom Startmodell weder in seiner Lage noch in seiner Amplitude erfaßt. Da über die Ursache dieses zweiten Minimums an dieser Stelle nur spekuliert werden kann, wird zunächst versucht, die Vergleichsschwere auch bezüglich des zweiten Minimums so gut wie möglich nachzumodellieren. Die physikalische und geologische Bedeutung des zweiten Minimums wird in der Diskussion des Abschlußmodells herausgestellt.
Der Grund für die positiven Abweichungen im Zentrum liegt vermutlich in der unzureichenden Kenntnis der krusteninternen Strukturen. Die Abweichungen im Außenraum hingegen liegen offenbar in Unzulänglichkeiten in der Beschreibung der Schwellenstruktur in größeren Tiefen. Das Modell ist derart zu verändern, daß die positive Abweichung im Zentrum reduziert wird und die negative Abweichung in den Außenbereichen zurückgeht.
Anhaltspunkte für die Modellanpassung gibt der Verlauf der Modellschwere in dem in 220 km Entfernung parallel zur Schwellenachse verlaufenden Profil. Hier sind allein die regionalen Störkörper größerer Tiefen wirksam. Dies trifft für das Profil entlang der Schwellenachse aufgrund der dort vorhandenen (zum Teil) kompensierten Topographie nicht zu. Die Form der Modellkörper senkrecht zum Streichen der Schwellenachse ist im wesentlichen achsensymmetrisch zur Schwellenachse.
8.2. Das Geoid-Signal des Mantel-Plume-Hot-Spot-Modells
Für eine weitere Kontrolle des Modells liegt es nahe, das Geoid hinzuzuziehen. Hier liegt gemäß Abb. 35 ein Vergleichsfeld vor. Es sind dies neben den oben genannten Ergebnissen aus Tomographie, theoretischen Modellrechnungen u. a. die einzigen Daten, die zur Eingrenzung der Modellstruktur herangezogen werden können. Wie bereits durch Abb. 44 angeschnitten, ist die Abbildung eines Dichtemodells auf eine Meßkurve nicht eindeutig, so daß zusätzliche Randbedingungen die Aussagekraft des Modells verstärken.
Obwohl das Geoid bereits durch Abb. 35 in die Diskussion eingeführt wurde, sei hier noch einmal sein Unterschied zur Schwere dargelegt. Bei der Schwere handelt es sich um ein Maß für die Kraft, die die Erdmasse an einer bestimmten Raumkoordinate auf eine Probemasse ausübt. Das Geoid stellt ein Maß für die Figur der Erde dar. Hierbei handelt es sich um eine Äquipotentialfläche in der Nähe des Meeresniveaus, die die wirkliche Erdoberfläche als geschlossene Fläche ohne Ecken und Kanten (mathematische Oberfläche) wiedergibt. Im Gegensatz zu einer rein geometrischen Bestimmung der Figur der Erde (physikalische Oberfläche) gehen in die Definition des Geoids (mathematische Oberfläche) auch Massenunregelmäßigkeiten im Untergrund ein. Das Schweresignal eines Störkörpers klingt quadratisch mit zunehmender Entfernung ab, das des Geoids hingegen nur linear. Darin manifestiert sich die Eigenschaft, daß das Geoid insbesondere tiefere und ausgedehntere Strukturen repräsentiert. Dies kommt den Untersuchungen der vorliegenden Arbeit sehr entgegen.
Aus den ersten Gliedern der Reihenentwicklung für das Gravitationspotential im Außenraum der Erde folgt unter Berücksichtigung der Zentrifugalbeschleunigung eine Gleichung für ein sogenanntes Referenzellipsoid (Sphäroid). Die Abweichungen des Geoids von dieser Niveaufläche bezeichnet man als Geoid-Undulationen. Eine horizontale Schichtlagerung liefert kein Geoidsignal. Erst eine anomale, von der horizontalen Lagerung abweichende Massenverteilung führt zu einer Geoidundulation.
Um eine Abschätzung für das Geoidsignal der 3D-Mantel-Plume-Hot-Spot-Struktur zu bekommen, wurde die den Modellschwereberechnungen der Abb. 55, Abb. 56, Abb. 57 und Abb. 58 zugrundeliegende Dichtestruktur für ein Programm (Fliedner, 1991) aufbereitet, das die Geoid-Undulationen nach dem Verfahren von Chapman (1979) berechnet. Das Programm berechnet die Geoidundulation zweidimensional. Damit läßt sich eine Abschätzung darüber erzielen, inwieweit das Modell die Wirklichkeit wiedergeben kann.
Im Gegensatz zu den Schwereprogrammen (2D nach Talwani (1959) bzw. 3D nach Götze und Lahmeyer (1988)), die absolute Dichten für die einzelnen geologischen Körper akzeptieren, arbeitet das vorliegende Geoid-Programm von Fliedner (1991) mit relativen Dichtekontrasten, die gegenüber einer ungestörten horizontalen Schichtlagerung anzusetzen sind. Es besteht eine Unsicherheit in den Ergebnissen in den Randbereichen des Modells. Der Randfehler wird gering gehalten, indem die horizontale Lagerung bis ins Unendliche (im Rechner: weit entfernter Punkt, an dem sich alle horizontalen Schichtgrenzen schneiden) extrapoliert wird. Auf diese Weise entsteht kein Geoidsignal durch eine senkrechte Modellbegrenzungslinie. Außerdem besteht nach Fliedner (1991) eine besondere Schwierigkeit bei Geoidmodellen darin, daß im Gegensatz zur Schwere die nichtlokale Wirkung einzelner Polygonseiten dazu führt, daß die Änderung der Modellgeometrie an einer Stelle erhebliche Auswirkungen auf die Gestalt der gesamten Geoidkurve haben kann. Dies macht das Vergleichen einzelner Kurven untereinander schwieriger. Die Strukturen der Dichteverteilung (absolute Werte) aus den Abb. 55, Abb. 56, Abb. 57 und Abb. 58 wurden den Anforderungen des Geoid-Programms (relativer Dichtekontrast gegenüber zu erwartender Schichtdichte nach Abb. 69) entsprechend umformatiert. Damit ergaben sich dann die in Abb. 68 vorgestellten Geoidundulationen für die einzelnen Körper und Schichtgrenzen.
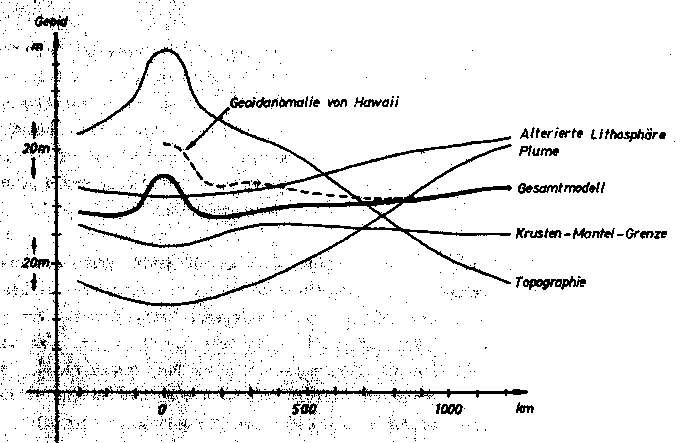
Abb. 68. Geoidsignale der Strukturen nach Abb. 55 (Krusten-Mantel-Gren-
ze), Abb. 56 (alterierte Lithosphäre), Abb. 57 (Plume) und
Abb. 58 (Gesamtmodell, wobei hier der Wasserkörper nicht als
Gesteinskörper gilt). Hinzu kommt durch die Berücksichtigung
des Wasserkörpers die topographische Wirkung (vgl. auch
Abb. 41). Gestrichelt eingetragen ist die zentrale Geoidanoma-
lie von Hawaii nach Monnereau und Cazenave (1990).
Vergleicht man die in Abb. 68 dargestellten Kurven untereinander und mit Abb. 35, so ergeben sich die folgenden Ergebnisse. Die Modellrechnungen zeigen nach Abb. 68 ein lokales Geoidmaximum über der Inselkette, das die zentrale Vulkankettenbathymetrie der Schwelle widerspiegelt, und ein regionales Geoidminimum des Schwellenbereiches (Möglicherweise handelt es sich hierbei aber auch um einen Artefakt (insbesondere für Entfernungen von mehr als 800 km von der Schwellenachse) als Folge der mit dem Programm zur Geoidberechnung aufgetretenen Probleme (siehe oben)). Nach Abb. 68 wird das Geoidsignal im wesentlichen durch die (sowohl lokale als auch regionale) Topographie (+) und den Mantel Plume (-) bestimmt.
Da nach Abb. 68 allein die topographische Anomalie der Hot-Spot-Vulkane aus dem Gesamtmodellgeoid hervorgeht, heben sich alle übrigen in Abb. 68 modellierten Effekte auf. Somit ist das Vorhandensein alterierter Lithosphäre und des Mantel Plumes direkt übereinander mit maximalen Mächtigkeiten wie in Abb. 58 als Geometrie dargestellt nicht wahrscheinlich. Die danach zu erwartende regionale Geoidanomalie fällt niedriger aus als es die Abb. 35 oder die Kurve von Monnereau und Cazenave (1990) zeigt. Geht man jedoch von einer Aufdomung der gesamten Lithosphäre im Bereich des Plumeaufstiegs aus, entstünde durch den relativen Massenüberschuß (aufgestiegene Asthenosphäre, aufgestiegene Lithosphäre) ein positiver Beitrag zum Geoid, welcher mit den Massendefiziten der alterierten Lithosphäre und des Plumes zu verrechnen wäre. Da im Geoidmodell der Wasserkörper nicht wie in der Bouguerschweremodellierung durch Gestein ersetzt wird, verbleibt ein regionaler Bereich von Massenüberschuß durch die Schwelle, der das regionale Geoidmaximum in Abb. 35 ausmacht. Das Geoid entspricht in diesem Sinne der Freiluftanomalie. Die Aufdomung der gesamten Lithosphäre im Bereich des Plumeaufstiegs wird in der Entwicklungsphase des 3D-Modells mit einbezogen.
Die Aufdomung ohne die alterierte Lithosphäre kann jedoch auch nicht vorliegen, da dies im Widerspruch zu der berechneten langwelligen Bougueranomalie liegt. Danach müssen Massendefizite im Untergrund überwiegen. Damit kann es nicht sein, daß ein vorhandener Plumeaufstieg einfach zu einer Aufwölbung der Lithosphäre führt. Dieser Vorgang würde zwar einen negativen Beitrag durch den Plume verursachen, der positive Beitrag der Aufwölbung übersteigt jedoch die Plume-Effekte, so daß mit einer positiven Anomalie zu rechnen gewesen wäre (vgl. Kap. 8.3.).
Das beobachtete, gefilterte Geoid nach Abb. 35 sowie das Geoid nach Monnereau und Cazenave (1990) zeigt im Untersuchungsgebiet um Hawaii im wesentlichen eine positive Geoidanomalie, deren Amplitude bei etwa 5m liegt. Diese Tatsache gibt einen Hinweis darauf, daß das Modell aus Abb. 58 noch einer Verbesserung hinsichtlich positiver Geoidbeiträge zu unterziehen ist. Dies geschieht im Falle des 3D-Modells dadurch, daß die maximalen Effekte aus Plume-Massendefizit und Lithosphären-Massendefizit räumlich voneinander getrennt werden (vgl. Abb. 60), so daß die maximalen Effekte nicht gleichzeitig in die Geoidanomalie eingehen. Auf diese Weise reduzieren sich die Massendefizite aus Abb. 62 derartig, daß nunmehr regional die Geoidanomalie im positiven Sinne ansteigt, so daß etwa der von Monnereau und Cazenave (1990) gegebene regionale Geoidverlauf sowohl im Hot-Spot-Zentrum als auch im westlichen Teil der Schwelle vorliegen sollte.
An dieser Stelle muß noch hinzugefügt werden, daß Abb. 35 nicht nur die Geoidanomalie der Schwelle beinhaltet, sondern auch Geoidanomalien, die in der Nachbarschaft der Schwelle liegen, aber dabei nicht im Zusammenhang mit der Schwelle stehen. McNutt und Shure (1986) weisen z. B. daraufhin, daß das Geoid-Tief südöstlich der Schwelle die Amplitude des Schwellengeoids drückt. Dies zeigt, daß abgesehen von unsicheren Methoden mathematischer Filter zusätzlich Fremdeffekte, also die Überlagerung verschiedener Anomalien, die Interpretation der Geoiddaten erschweren (vgl. auch Sleep, 1990).
8.3. Überlegungen zur Verfeinerung der Modellstruktur
8.3.1. Allgemeine Randbedingungen
Die Verbesserung des Startmodells kann im wesentlichen auf zwei Arten erfolgen. Einerseits können die Dichtewerte und andererseits die Geometrie der einzelnen Strukturen geändert werden. Eine Änderung der Dichtewerte hat zur Folge, daß sich die betreffende Struktur mit einer anderen Schwereanomalieamplitude ins Modell einfügt. Bei der Änderung der Geometrie hingegen verändert sich die Wellenlänge sowie die Form der Anomalie. Die Modellierung konzentriert sich damit auf folgende Fragestellungen:
- wie hoch reicht die alterierte Lithosphäre?
- wo kommt es überhaupt zu einer Alteration?
- wo genau liegt die Plume-Struktur?
- welche Form hat die Plume-Struktur?
- liegt eine Aufwölbung der Lithosphäre durch Plumeeinwirkung vor?
Im Rahmen der Verbesserung des Startmodells ist keine Auflösung von Strukturen im 10km- bis 100km-Bereich möglich. Daher kann das Dichtemodell beispielsweise keine Aussagen über die Strukturen einzelner Vulkanschlote bringen. Auch eine genaue Modellierung möglicher Strukturen, die im Zusammenhang mit einem Aufstieg von Schmelzen direkt über dem Zentrum des Mantel Plumes stehen, kann daher nicht gegeben werden.
Das in Kap. 8.1.3. vorgestellte Startmodell entstand empirisch aus den verschiedenen im Text enthaltenen Angaben über Mantel Plumes und über Hawaii. Die wichtigsten Parameter, Ideen und Randbedingungen, denen das zu bestimmende Endmodell neben einer möglichst guten Anpassung an die Vergleichsschwere genügen soll, listet die Zusammenstellung nach von Herzen et al. (1989), wonach ein gutes Modell für die Hawaii-Schwelle folgende Beobachtungen erklären können muß:
- der abrupte Anstieg der Schwelle südöstlich von Hawaii,
- die allmähliche Absenkung nordwestlich längs der Schwellenachse
nach dem Passieren des Mantel Plumes,
- die Abwesenheit einer signifikanten Wärmeflußanomalie im älteren
Bereich der Schwelle,
- Kompensation der Schwelle unter oder im unteren Bereich der
Lithosphäre.
8.3.2. Relative Dichteanomalien zwischen Kruste und Mantel
Im Zusammenhang mit Abb. 69 werden jetzt die einzelnen relativen Dichteinhomogenitäten herausgestellt. Die in Abb. 62 dargestellten Körper wurden mit einer absoluten Dichte klassifiziert. Bereits die Kalkulation der Geoid-Effekte in Kap. 8.2. erforderte jedoch die Angabe relativer Dichteanomalien. Dabei wird von einer horizontalen Schichtlagerung im ungestörten Fall ausgegangen. Eine solche Anordnung führt weder zu einer Schwere- noch zu einer Geoidanomalie. Die Körper aus Abb. 62 müssen für die Bestimmung der Lage der relativen Dichteanomalien im Modell mit einer horizontalen Referenzschichtlagerung, die den ungestörten Fall repräsentiert, verglichen werden. Auf diese Weise erkennt man, wo relativ zur horizontalen Lagerung Überschuß- und Defizitmassen auftreten. Eine solche Gegenüberstellung zeigt die Abb. 69 für die in Abb. 62 enthaltenen Strukturelemente.
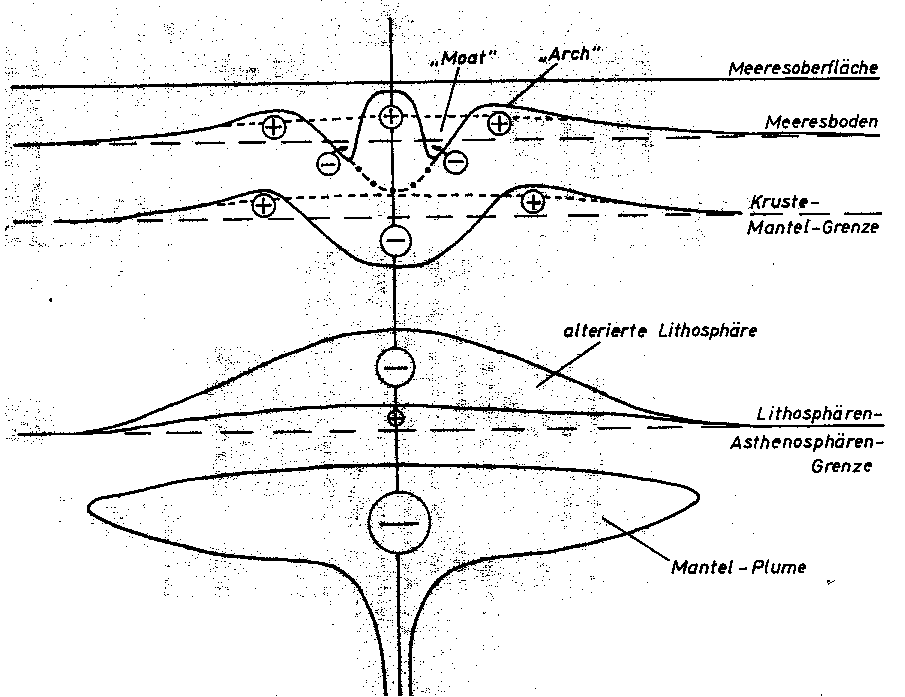
Abb. 69. Verteilung relativer Dichteanomalien, die als Differenz zu ei-
ner horizontalen Schichtlagerung auftreten, für die Modellele-
mente in Abb. 62. Massenüberschüsse sind dabei durch "+" und
Massendefizite durch "-" gekennzeichnet. Die lang gestrichelten
Linien kennzeichnen die horizontale Lage von Grenzen, die kurz
gestrichelten Linien den Bereich der Schwellung ohne Einflüsse
der Biegung der Kruste durch die Vulkanauflast. Die Strukturen
sind nicht maßstabsgetreu zueinander wiedergegeben.
Durch die Berechnung der "Bouguerschwere" wurde die Topographie "weggerechnet". In erster Näherung setzt sich die Topographie aus dem Bereich der Vulkangebäude und dem Verlauf der Krustenoberfläche, dem Meeresboden abseits der Vulkane, zusammen. Bei einer gleichmächtigen Kruste bildet sich die Topographie, die sich bei der Wegnahme der Vulkanauflasten ergeben würde, aufgrund der Parallelverschiebung auf die Krusten-Mantel-Grenze ab. Damit liegt im Bereich der Vulkaninseln eine scheinbare Krustenverdickung vor, die sich aus der normalmächtigen Kruste plus der Vulkanauflast ergibt. Da die Vulkanauflast die Kruste in das Lid gedrückt hat, liegt letztendlich hier ein relatives (lokales) Massendefizit und damit ein Bouguerminimum vor. Die negativen Massenanomalien, die sich in der Freiluftanomalie um die Inseln herum zeigen, obwohl dort keine topographische Auflast mehr liegt, vgl. Abb. 36, sind die Folge der durch die Vulkanauflast hervorgerufenen Krusteneindellung. In der Darstellung der Bougueranomalie verschmelzen diese zu dem bereits von der Krustenverdik-kung, die aus normal mächtiger Kruste plus Vulkanauflast zusammengesetzt ist, hervorgerufenen Bouguerminimum.
Aufgrund der Balkentheorie kommt es in einem Abstand von der Vulkanauflast dann zu einer Krustenaufbiegung, in die sich dichteres oberes Mantelmaterial schiebt. Demnach kommt es hier zu einer positiven Anomalie in einem Abstand von mehreren 100 km um die Vulkankette herum. Weitere positive Bougueranomalien ergeben sich aus einer Aufwölbung der gesamten Lithosphäre infolge eines Mantel-Plume-Aufstiegs. Dies zeigt Abb. 70a in Kap. 8.3.3.. Danach drängt asthenosphärisches und damit dichteres Material die Lithosphäre nach oben. Isostatische Betrachtungen anhand ausgewählter 2D-Profile des Abschlußmodells werden in Kap. 9.2. erörtert.
8.3.3. Relative Dichteanomalien aus der Plume-Lithosphären-
Wechselwirkung
Die wesentlichsten defizitären Massenanomalien jedoch rühren nach Abb. 69 aus der unteren Lithosphäre und der oberen Asthenosphäre her. Sie übertreffen die Effekte positiver Massenanomalien durch Aufwölbung der gesamten Lithosphäre mehrfach. Im sublithosphärischen Bereich befindet sich die negative Anomalie des Mantel Plumes. Direkt darüber kommt eine negative Anomalie durch eine alterierte Lithosphäre nach Kap. 7.1.2. hinzu. Man erkennt hieran bereits sehr deutlich, daß die Bougueranomalie im großen und ganzen vom Plume selbst beziehungsweise seiner Wechselwirkung mit der Lithosphäre herrührt. Demnach sind den Plume-Lithosphären-Wechselwirkungen besondere Aufmerksamkeit zu widmen. Auch im Hinblick auf den zeitlichen Verlauf der Wechselwirkung von Plume und Lithosphäre längs der Schwellenachse muß dies beachtet werden (vgl. Abb. 70c).
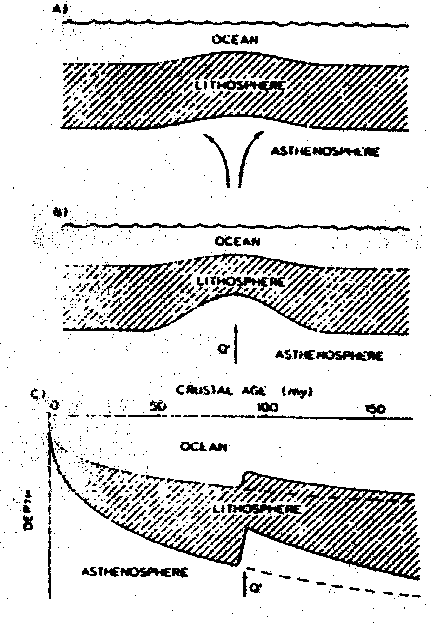
Abb. 70. Wechselwirkung von Mantel Plume und Lithosphäre.
a. Eine Lithosphäre konstanter Mächtigkeit wird durch einen
Mantel Plume hochgebogen;
b. Asthenosphärisches, heißes Material und damit Material ver-
minderter Dichte dringt in die Lithosphäre ein und bewirkt
ein "lithospheric thinning".
c. Die Wirkung der Abkühlung der Lithosphäre in Richtung der
Schwellenachse. Der Meeresboden sinkt schneller ab als es
vom Krustenalter zu erwarten gewesen wäre.
(nach Detrick und Crough, 1978).
Die Abb. 70 stellt allgemein die Wechselwirkung von Aufheizung und Abkühlung dar. In Abb. 70c deutet der mit einem "Q" gekennzeichnete Pfeil eine plötzliche "Injektion" von Wärmeenergie an. Diese Injektion findet lediglich an dieser einen Stelle statt und ist ein Ereignis von kurzer Dauer. Nach diesem Ereignis beginnt sogleich der Abkühlungsprozeß, welcher durch das rasche Absinken des Ozeanbodens und das Verdicken der Lithosphäre angedeutet wird. Es sind bisher keine seismischen Untersuchungen durchgeführt worden, aus denen Aussagen über die tiefere Struktur der Kruste und der Lithosphäre längs der Schwellenachse gemacht werden können. Aus der beobachtbaren Absenkung der Inseln und Seamounts kann auf eine Absenkung der Kruste und eine Verdickung der Lithosphäre infolge der Abkühlung geschlossen werden.
Der plötzliche Anstieg an der Stirnseite der Schwelle östlich der Insel Hawaii kann z. T. durch die Flexur erklärt werden, die senkrecht zur Schwellenachse durch die Vulkanauflast wirksam ist. Östlich der Insel Hawaii befinden sich (noch) keine nennenswerten Auflasten, so daß die Effekte durch die Vulkanauflast erst von der Insel Hawaii an westlich beobachtbar sind. Das allmähliche Absinken der Inseln wird im 3D-Modell im westlichen Teil der Schwelle berücksichtigt, indem sich dort die Kruste verdickt und dabei einsinkt. Im westlichen Teil verringert sich zudem die Amplitude der Inseln (nicht der Seamounts) im wesentlichen durch die exogenen Kräfte der Erosion. Außerdem liegt hier nach der Modellidee (Abb. 60), die im wesentlichen auch das Abschlußmodell bestimmt, noch der Bereich der alterierten Lithosphäre, der einem Einsinken der Kruste vorerst entgegenwirkt.
Geht man von einem normalen Dichtegradienten (Zunahme der Dichte mit der Tiefe) aus, so kann ein Einsinken der gesamten Lithosphäre infolge Abkühlung nicht die Beträge annehmen, die bei einer gegenüber der unteren Lithosphäre verminderten Dichte der oberen Asthenosphäre zu erwarten sind. Dem Einsinken der Lithosphäre steht der Bereich der alterierten Lithosphäre entgegen. Damit läßt sich im Bereich der Schwelle keine Unterscheidung zwischen dem Abklingen des Bereiches alterierter Lithosphäre und dem möglichen Einsinken der Lithosphäre treffen. Die Grenze zwischen der Lithosphäre und der Asthenosphäre ist zwischen dem Plume und der alterierten Lithosphäre damit undefiniert. Ein möglicher positiver Beitrag in der Massenbilanz (vgl. Abb. 69) durch das Anheben der Lithosphäre bei einem normalen Dichtegradient (Zunahme der Dichte mit der Tiefe) kann außerdem mit dem Beitrag der alterierten Lithosphäre direkt verrechnet werden. Aus diesen Gründen wird die Modellierung einer unter dem Einfluß des Plume-Auftriebs aufgewölbten Lithosphären-Asthenosphären-Grenze nicht explizit erforderlich.
Verschiedene Autoren haben sich mit der Wechselwirkung von Plumes und der Lithosphäre auseinandergesetzt (z. B. Ribe und Christensen, 1994; Saunders et al. 1992). Keiner der Autoren hat jemals eine Angabe darüber gemacht, in welcher Größenordnung die damit verbundene Dichteänderung (sowohl zeitlich als auch räumlich) der Lithosphäre durch den Plume liegt. Die ausgeworfenen primordialen Zusammensetzungen vulkanischer Laven verweisen auf einen Transport durch die gesamte Lithosphäre, der nach z. B. Glahn et al. (1992) oder Hoernle et al. (1991) nicht spurlos durch die Lithosphäre hindurchgeht. Dies wird sich in irgendeiner Form der Dichteerniedrigung bemerkbar machen. Obwohl Angaben über konkrete Dichtewerte für eine alterierte Lithosphäre in der Literatur nicht zu finden sind, läßt sich eine negative Dichteanomalie der Lithosphäre im Bereich der Plume-Einwirkung bereits aus dem Eindringen heißen Materials aus der Asthenosphäre in die kühlere Lithosphäre ableiten. Dies bedeutet im Zusammenhang mit der Erstellung des 3D-Dichtemodells für den Hawaii-Mantel-Plume-Hot-Spot, daß dort modellierte Körper lediglich die Dichteanomalien im Vergleich zu einer ungestörten, horizontalen Lage darstellen. Die Ansprache einzelner Körper in Form von Asthenosphäre und Lithosphäre im Bereich der Plume-Lithosphären-Wechselwirkung ist über die Definition einzelner Dichten nicht möglich, da die verschiedenen Dichten eben nicht nur von der chemischen Zusammensetzung, sondern auch noch von Druck und Temperatur abhängig sind.
8.4. Die Erarbeitung des Abschlußmodells
8.4.1. Allgemeines zur weiteren Modellentwicklung
Zunächst werden Begriffe definiert, die der Beschreibung von Orten im Bereich der Hawaii-Schwelle dienen. Die Form der Schwelle ist langgestreckt. Die Streichrichtung der Schwellenachse liegt etwa Ostsüdost-Westnordwest. Im Hinblick auf die Strömungsrichtung der pazifischen Platte in die gleiche Richtung bedeutet
"stromabwärts" in die Strömungsrichtung nach Westnordwest,
"stromaufwärts" gegen die Strömungsrichtung nach Ostsüdost,
der "vordere" Bereich der Schwelle der im Südosten gelegene und
der "hintere" Bereich der im Nordwesten gelegene Bereich der Schwelle. Zur Entwicklung des Abschlußmodells wird eine Anpassung der Modellschwere an eine "Vergleichsschwere" vorgenommen. Als Vergleichsschwere dient die in Abb. 71 dargestellte regionale Bouguerschwere, die aus einer Tschebyschev-Approximation vom Grad 9 hervorgeht (vgl. Abb. 52 in Kap. 6.3.).
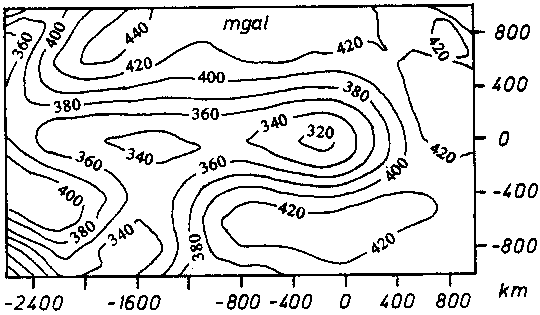
Abb. 71. Die regionale Bouguerschwere als Vergleichsschwere. Der Isoli-
nienabstand beträgt 20 mGal. Die gepunkteten Linien zeigen für
konstante y-Werte die Lage der modelldefinierenden Profile an.
Außerdem gepunktet gekennzeichnet sind die Schwellenachse (x=0)
sowie die Lage eines Profils parallel zur Schwellenachse (x =
220 km), auf das im Text oft verwiesen wird.
Mit der vorliegenden Arbeit soll eine bessere Evidenz für den Mantel Plume gefunden werden. Die regionale Vergleichsbouguerschwere sollte dafür durch möglichst wenige und einfache Körper modelliert werden. Auf diese Weise läßt sich sehr gut feststellen, ob und inwieweit die Vergleichsschwere mit einem Mantel Plume vereinbar ist. Der Hawaii-Hot-Spot eignet sich aufgrund der im ersten Teil der vorliegenden Arbeit herausgestellten isolierten Stellung abseits von Fremdeinflüssen anderer tektonischer Prozesse gut zur Untersuchung grundlegender Beziehungen zwischen Vulkanismus, Schwellenbildung und Mantel Plumes.
Die Körper, aus denen das 3D-Modell zusammengesetzt werden soll, müssen im Programmsystem IGAS durch eine konstante Dichte modelliert werden. In Wirklichkeit jedoch nimmt die Dichte stets mit der Tiefe zu bzw. ist die Asthenosphäre im ozeanischen Milieu unterhalb der Lithosphäre von verminderter Dichte (vgl. Kap. 7.2.). Die Grenze zwischen Lithosphäre und Asthenosphäre ist nicht scharf ausgeprägt (Janle und Meissner, 1986; Turcotte, 1979). Es liegt ein kontinuierlicher, stetiger Dichtegradient vor. Jedoch ist es für die Überlegungen der vorliegenden Arbeit nicht wichtig, verschiedene geologische Horizonte zu modellieren. Vielmehr kommt es auf die Störung durch Fremdkörper wie dem Mantel Plume an, wobei die Störkörper in der Regel keine einheitliche Dichte aufweisen werden.
Der Mantel Plume besteht aus dem sublithosphärischen Pilz und der Aufstiegszone des Plume-Materials. Der Bereich des Sublithosphärenpilzes beinhaltet nach Li und Spohn (1991) partielle Schmelzen. Der Aufstiegskanal wird von vielen Autoren als dünn und damit vernachlässigbar angenommen. Ein Aufstieg von Material setzt eine Instabilität voraus. Das Aufsteigen des Materials kann nur möglich sein, wenn das aufsteigende Material durch erhöhte Temperatur oder veränderte chemische Zusammensetzung oder beides eine gegenüber der Umgebung verminderte Dichte aufweist. Dieser Dichtekontrast muß entlang der gesamten Strecke des Aufstiegs vorhanden sein. Andernfalls würde der Aufstiegsprozeß zum Erliegen kommen. Diese Bedingungen sind bei einem adiabatischen Aufstieg, der für die Mantel-Plume-Dynamik gilt, gegeben. In diesem Sinne kann der Mantel Plume, auch wenn seine absolute Dichte in den unteren Bereichen größer als in den oberen ist, mit einer konstant über alle Tiefenbereiche angenommenen relativen Dichtedifferenz als geschlossener Körper modelliert werden.
Somit reicht es völlig aus, die relativen Dichteänderungen gegenüber der ungestörten Umgebung für alle Modellgeometrien zu vereinbaren. Alle Störkörper, also z. B. auch die Mantel-Plume-Struktur, werden durch Dichtekontraste zu benachbarten horizontal gelagerten Schichten definiert und mit einer relativen Dichte belegt. Damit entfällt das Betrachten von Körpern mit absoluten Dichteunterschieden.
Damit reduzieren sich die zu modellierenden Körper auf drei:
- den Bereich der Krusten-Mantel-Grenze,
- dem Bereich alterierter, durch eine Plume-Lithosphären-Wechselwirkung (plume-lithosphere-interaction PLIA) hervorgerufene anomale Lithosphäre, evtl. auch eingedrungenes asthenosphärisches Material) und
- der Mantel-Plume-Struktur selbst.
Im Zuge der Veränderungen des Startmodells reichte das Spektrum der Dichten für die Kruste von 2,67 g/cm3 bis zu 3,00 g/cm3, das der Lithosphärendichte von 3,24 g/cm3 bis zu 3,28 g/cm3 (vgl. Kap. 7.2. und 8.4.2.). Die Modellierung der Krusten-Mantel-Grenze wurde schließlich mit einem abgeschwächten Dichtekontrast durchgeführt, da es auf die relativen Dichtekontraste beiderseits der Grenzfläche mehr ankommt als auf den Dichtekontrast, der sich durch Durchschnittswerte der beiden an der Grenzfläche beteiligten Strukturelemente ergibt. Der Plume wurde mit relativen Dichten gegenüber der Asthenosphäre von -0,01 g/cm3 bis zu -0,03 g/cm3 gerechnet. Veränderungen der Plume-Geometrie und das Verschieben der Lage der das Modell definierenden Profile wurden für eine bessere Anpassung der Modellschwere an die Vergleichsschwere ausprobiert. Außerdem wurden Modelle mit und ohne Aufstiegskanal ausprobiert. Dabei zeigte sich, daß die Modellschwere eines schmalen Aufstiegskanals vernachlässigbar und die eines breiten Aufsteigskanals aber auch durch eine veränderte Form des Sublithosphärenpilzes modelliert werden kann, so daß die Modellierung des Plumeaufstiegskanals nicht zwingend wird. Im Rahmen der Modellentwicklung ließ es das Programm IGAS nicht zu, mit Dichteerhöhungen oder -erniedrigungen von weniger als 0,01 g/cm3 arbeiten zu können. Dadurch ließen sich keine weiteren Verfeinerungen erzielen, die für diese Betrachtung aber auch nicht nötig sind.
Als bestes Ergebnis aus der Variation der Modellstruktur für den hawaiianischen Mantel-Plume-Hot-Spot geht das im nächsten Kapitel beschriebene und diskutierte Modell als Abschlußmodell hervor.
8.4.2. Die Struktur des 3D-Dichtemodells
Das Abschlußmodell setzt sich aus Strukturen, die durch einen relativen Dichtekontrast beschrieben worden sind, zusammen. Im einzelnen betragen die relativen Dichten des Abschlußmodells:
= -0,24 g/cm3 für die Krusten-Mantel-Grenze,
= -0,03 g/cm3 für die alterierte Lithosphäre und
= -0,02 g/cm3 für den Mantel Plume.
Diese Werte sind durch die folgenden Dichtewerte geometrischer Körper realisiert worden:
Kruste: 3,00 g/cm3,
Lithosphäre ohne Kruste: 3,24 g/cm3,
alterierte Lithosphäre: 3,21 g/cm3,
Asthenosphäre: 3,36 g/cm3,
Mantel Plume: 3,34 g/cm3.
Die relative Dichte für den Mantel Plume entstammt dem Ansatz von Li und Spohn (1991) (vgl. Gleichung (2) in Kap. 5.4.1.). Diese Dichtedifferenz entspricht nach Gleichung (1) in Kap. 5.4.1. bei einer Manteldichte von 3,3 g/cm3
einer Überschußtemperatur des Mantel Plumes von T = 200 K. Die Dichte von = 0,24 g/cm3 für die Krusten-Mantel-Grenze geht auf ei-ne angenommene Dichte von 3,0 g/cm3 für die untere Kruste und eine angenommene Dichte von 3,24 g/cm3 für die obere Lithosphärenschicht nach Brinkmann (1984) bzw. Toksöz (1985) zurück. Die Dichte für die alterierte Lithosphäre wurde aus der Modellentwicklung empirisch gewonnen. Mit diesem Wert, der physikalisch noch erklärbar ist, konnte eine Anpassung der Modellschwere an die Vergleichsschwere erzielt werden.
Die Anpassung der Modellschwere an die Vergleichsschwere bestätigte die Möglichkeit der Existenz der angenommenen Körper. Dabei wurden Aussagen über ihre potentiellen relativen Dichten und ihre Form und Größenordnung gewonnen. Die genaue durch 15 Profile definierte 3D-Dichte-Modellstruktur des hawaiianischen Mantel-Plume-Hot-Spots zeigt die Abb. 72. Neben den 15 Profilen sind in Abb. 73 das Modellschwerefeld, drei parallel zur Schwellenachse verlaufende Profile und ein 3D-Blockmodell aufgeführt, damit die Struktur des 3D-Modells besser verdeutlicht werden kann. Eines dieser Profile verläuft entlang der Schwellenachse, die anderen verlaufen parallel dazu in Abständen von 220 km und 400 km.
Die Modellschwere gibt die Vergleichsschwere im Bereich der regionalen Schwelle in Amplitude und Wellenlänge gut wieder. Die Abweichungen der Modellschwere von der Vergleichsschwere, die sich in Abb. 72m zeigen, weisen auf Störungen durch andere Effekte, die hier nicht modelliert wurden, hin. Ein sich überlagerndes überregionales Feld weist im Bereich negativer x-Werte dann ein Minimum und im Bereich positiver x-Werte ein Maximum auf. Das relative Minimum um x=0 bleibt dabei erhalten. Diese Störungen zeigt Abb. 71. Die Schwelle wird durch die langgestreckte sich westwärts verjüngende Freiluftanomalie in Abb. 71 repräsentiert. Daneben liegen nach Abb. 71 südlich dieser Schwelle Störungen, die nicht in Zusammenhang mit der Hot-Spot-Tätigkeit gesehen werden. Die Nordseite der Schwelle wird nach Abb. 71 nicht durch Fremdeffekte gestört. Daher dient für die Modellierung insbesondere die Nordseite als Vergleichsfeld, da näherungsweise eine schwellenachsensymmetrische 3D-Dichtestruktur modelliert wurde.
In Abb. 73a ist die in den einzelnen Profilen bereits eingetragene Modellschwere als Feld über dem Bearbeitungsgebiet in Form eines Isolinienplanes aufgetragen. Die Differenzen zur in Abb. 71 dargestellten Vergleichsschwere zeigt die Abb. 73b. Zur besseren Veranschaulichung des Mo-
Abb. 72. (nachfolgende Seiten)
Die geometrische Modellstruktur des Abschluß-3D-Dichtemodells
des hawaiianischen Mantel-Plume-Hot-Spots in den 15 Profil-
schnitten. Die Darstellungen von a) bis q) geben die Struktur
der alterierten Lithosphäre und des Plumes an, die Darstellun-
gen r) bis v) die Geometrie der Krusten-Mantel-Grenze. Die Mo-
dellschwere ist über jedem Profil gestrichelt, die Vergleichs-
schwere durchgezogen eingetragen. Die Lage der Profile ist über
die y-Koordinate gemäß Abb. 59 definiert. Folgende Modelldich-
ten wurden verwendet:
Kruste: 3,00 g/cm
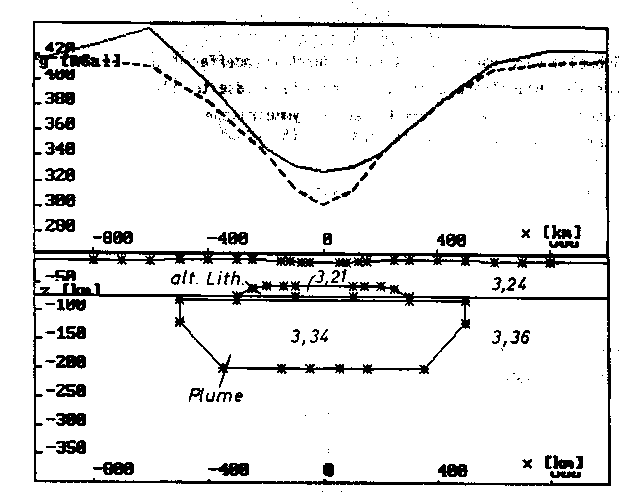
f) Querprofil bei y = 0 (im Hot-Spot-Zentrum).
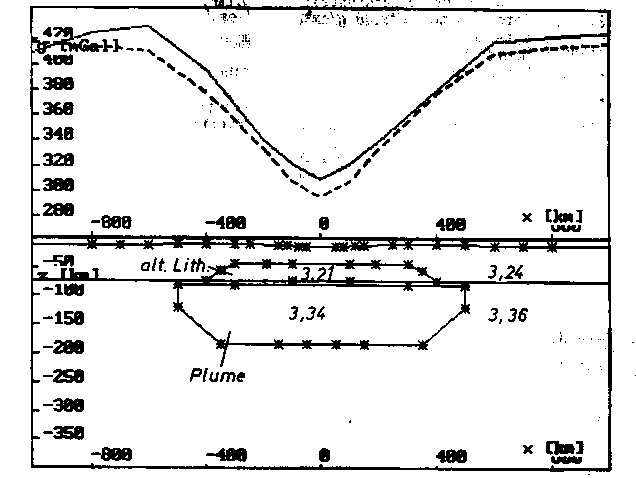
g) Querprofil bei y = 200 km (nahe dem Hot-Spot-Zentrum).
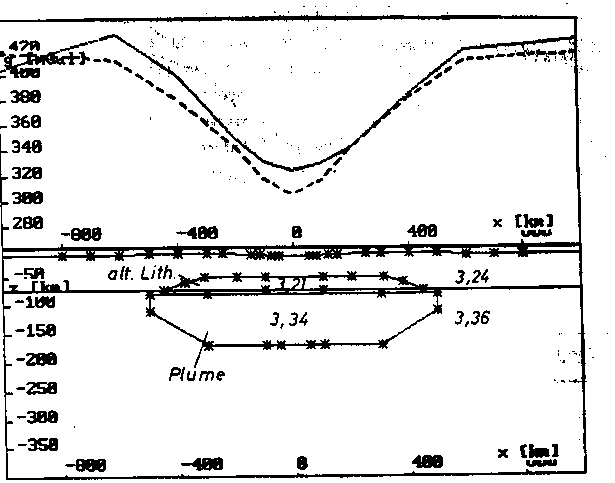
h) Querprofil bei y = 400 km (etwa im Verlauf des Profils A'B'
aus Kap. 5 ).
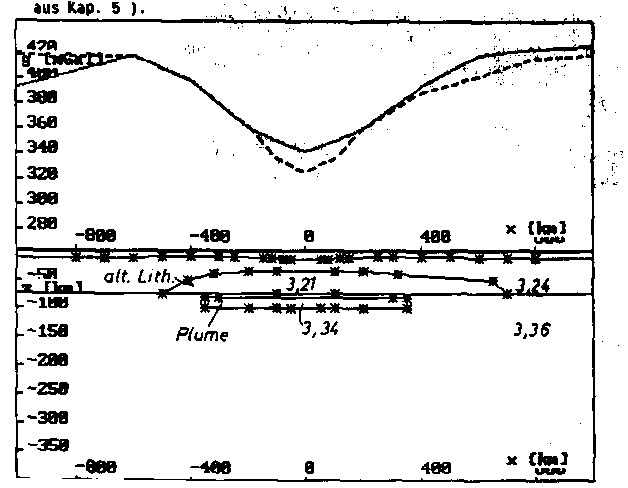
k) Querprofil bei y = 1000 km (stromabwärts im Bereich des abklingen-
den Plumes).
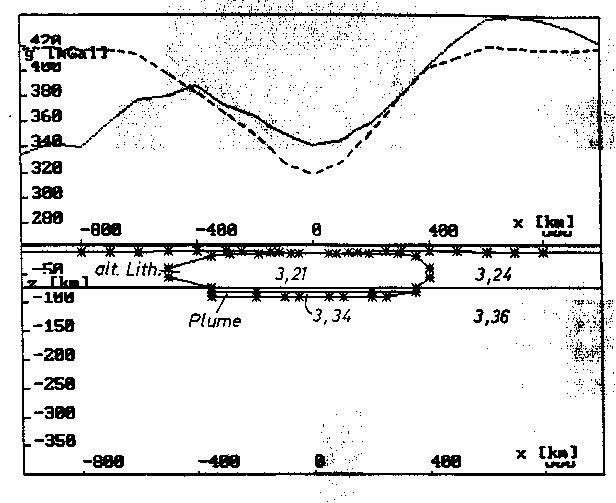
m) Querprofil bei y = 1900 km (im Bereich der alterierten Lithosphäre).
Die Abweichungen von Modell- und Vergleichsschwere um x = -800 km
sind auf Störungen von außerhalb, die nicht in Zusammenhang mit der
Kausalbeziehung zwischen Plume und Schwelle von Hawaii zu sehen sind,
zurückzuführen (vgl. auch Abb. 71 (Vergleichsschwere) und Abb. 73b
(Differenzfeld)).
dells sind noch drei Profile parallel zur Schwellenachse sowie ein 3D-Blockbild dargestellt worden.
Die Differenz zwischen der Modell- und der Vergleichsschwere längs der Schwellenachse (vgl. Abb. 73c) ist auf den lokal wirksamen Einfluß von Krustenstrukturen im Zusammenhang mit der Vulkankette im Schwellenachsenbereich zurückzuführen. Die Vergleichsschwere stellt ein regionales Schwerefeld dar. Die Anpassung der Modellschwere an die Vergleichsschwere erfolgte im wesentlichen durch die Modellierung regionaler Strukturen. Lokale Dichteanomalien berücksichtigt das Modell nicht, da über solche über den Bereich der Inseln hinaus nichts bekannt ist. Jedoch enthält das Modell insbesondere den Verlauf der Krusten-Mantel-Grenze, der für den zentralen Schwellenbereich aus den in Kap. 5.3. vorgestellten Ergebnissen abgeleitet wurde. In der weiteren Umgebung der Schwelle wurde die Krusten-Mantel-Grenze in 12 km Tiefe unter Normalnull (Durchschnittswert nach Sheriff (1984)) gelegt. Die geometrische Definition der Krusten-Mantel-Grenze aus dem Startmodell (vgl. Abb. 61r,s,t,u,v) wurde unverändert in das Abschlußmodell übernommen, da eine Anpassung der Modellschwere an die Vergleichsschwere mittels einer hypothetischen Tiefenlage der Krusten-Mantel-Grenze die Aussagen im Hinblick auf die zu modellierenden Effekte aus einer Plume-Tätigkeit nicht verändert. Im zentralen Bereich der
Abb. 73. (nachfolgend)
Die Modellschwere des Abschlußmodells.
a. das Modellschwerefeld des Bearbeitungsgebietes (die dicken
Linien stellen die Lage der in Kap. 9.2. diskutierten Profi-
le, längs derer die Massensummation (vgl. Kap. 9.2.) durch-
geführt wurde, dar; der Isolinienabstand beträgt 20mGal) und
b. das Differenzfeld aus dem Residuum von Modellschwere und der
Vergleichsschwere nach Abb. 71.
c. Profil im Verlauf der Schwellenachse (x = 0),
d. Profil parallel zur Schwellenachse bei x = 220 km,
e. Profil parallel zur Schwellenachse bei x = 400 km.
Für c,d und e ist die Modellschwere gestrichelt und die Ver-
gleichsschwere durchgezogen dargestellt.
f. 3D-Blockdarstellung des Abschlußmodells. Die Modellschwere
wird in ihren wesentlichen Eigenschaften von der Struktur
der alterierten Lithosphäre und des Mantel Plumes geprägt.
Die räumliche Anordnung und Geometrie wird hier verdeut-
licht. Das Hot-Spot-Zentrum liegt bei x=y=0. Der Mantel
Plume steigt unter dem geographischen Hot-Spot-Zentrum auf
und weist hier die größten Mächtigkeiten auf. Die Geometrie
der alterierten Lithosphäre liegt über dem Plume. Die ge-
zeigte Verbreiterung der alterierten Lithosphäre soll auf
einen möglichen Überlagerungseffekt mit der Murray-Fracture-
Zone (vgl. z. B. Abb. 33) hindeuten. Die Verbreiterung steht
nicht im Kausalzusammenhang zum Plume.
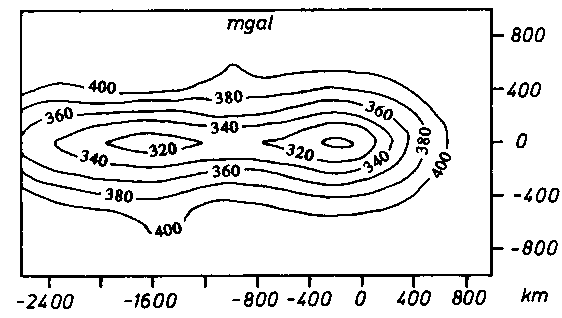
a) Das Modellschwerefeld des Abschlußmodells.
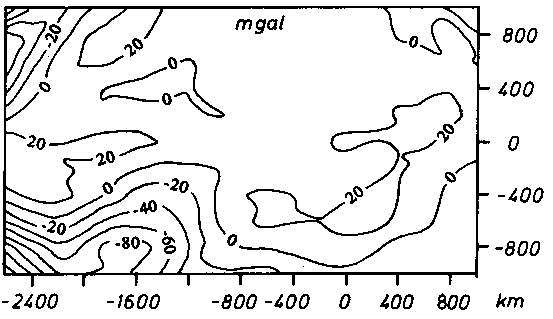
b) Differenzfeld zwischen Modell- und Vergleichsschwere.
c) Längsprofil im Verlauf der Schwellenachse (x=0). Die hier sichtbare
Differenz zwischen der Modell- und der Vergleichsschwere wird am
Schluß dieses Kapitels im Text erläutert.
d) Längsprofil parallel zur Schwellenachse bei x = 220 km.
e) Längsprofil parallel zur Schwellenachse bei x = 400 km.
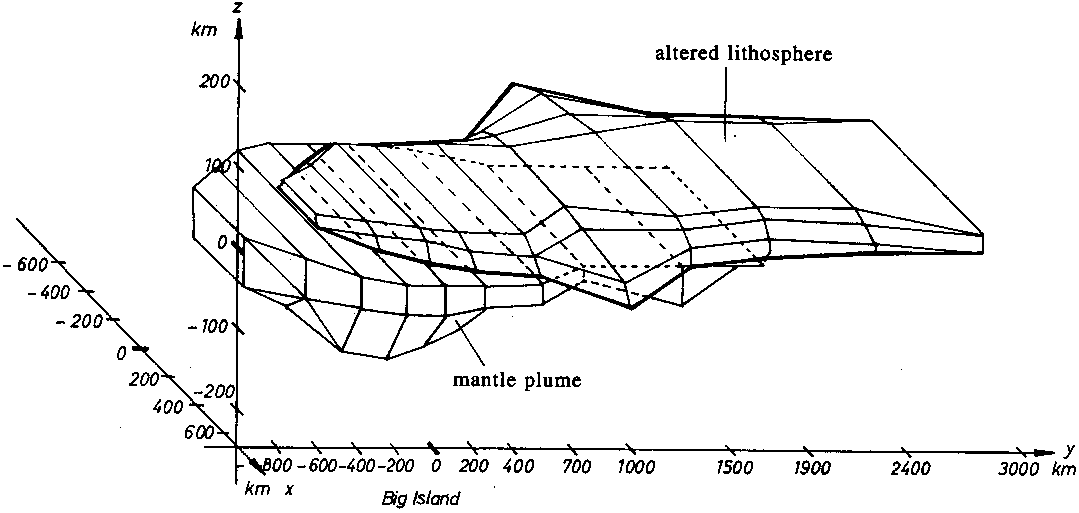
f) 3D-Blockdarstellung
des Abschlußmodells.
Schwelle spiegelt die Krusten-Mantel-Grenze die lokale Kompensation der Vulkanauflast wider. Diese ist somit in der Modellschwere durch ein lokales Schweredefizit längs der Schwellenachse (vgl. Abb. 63) enthalten, nicht aber in der regionalen Vergleichsschwere. Daher ergibt sich die Abweichung zwischen Modell- und Vergleichsschwere längs der Schwellenachse (vgl. auch Abb. 72 bei x=0). Die Form der Anomalie längs der Schwellenachse wurde jedoch wiedergegeben. Von den lokalen Störeinflüssen befreit sind die Darstellungen d) und e), da dort keine massiven Vulkangebäude die Schwelle beeinflussen.
zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite