zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite
5. Der Mantel-Plume-Hot-Spot von Hawaii
5.1. Allgemeine Informationen aus dem bisherigen Stand der
Forschung
Die Theorie der auf Mantel Plumes zurückgeführten Hot Spots geht auf die Arbeiten von Wilson (1963a,b) und Morgan (1971, 1972) zurück. Die Idee basiert im wesentlichen auf der Beobachtung, daß die Hawaii-Inseln nach Ostsüdosten hin immer jünger werden. Diese Tatsache kann jeder aufmerksame Naturbeobachter auch ohne fundierte geologische Kenntnisse im Gelände leicht feststellen. So erkannte z.B. James Dwight Dana auf seiner Expedition durch die Südsee im Jahre 1838 bereits die Altersabfolge der Inseln. Dana leitete diese einfach aus dem Grad der Erosion der Inseln ab. Es gibt aber auch eine Reihe weiterer Kriterien, aus denen sich dies feststellen läßt. So nimmt die Dominanz typischer, nahezu vegetationsloser Vulkanlandschaften an der Inseloberfläche nach Westnordwesten deutlich von Insel zu Insel ab. Außerdem erkennt der Botaniker eine wachsende Artenvielfalt nach Westnordwesten. Die Ureinwohner Hawaiis erkannten aufgrund derartiger Beobachtungen bereits die Natur ihrer Heimat lange vor der Ankunft der ersten weißhäutigen Menschen, wenngleich sie jedoch ihre Beobachtungen vollkommen anders interpretierten.
Die Hawaii-Emperor-Kette ist 6000 km lang und umfaßt mehr als 100 bekannte Vulkane, meist Seamounts. An ihrem Nordwest-Ende ist diese Kette 75 bis 80 Millionen Jahre alt. Nach Südosten hin wird sie progressiv jünger bis hin zum jüngsten Vulkan, Loihi Seamount (Watson und McKenzie, 1991). Dieser liegt östlich vor Big Island. Auf letzterer Insel liegt der ebenfalls noch aktive Vulkanismus von Mauna Loa und Kilauea. Die Schwelle um Hawaii weist eine Gaußkurvenform auf. Sie ist 1200 km breit und ihre größte Höhe beträgt etwa 1200m (Detrick und Crough, 1978). Die Wärmeflußanomalie (genauer: Anomalie der Oberflächenwärmeflußdichte) ist nicht größer als 5-10 mW/m2 (von Herzen et al., 1989). Dies wird auf die hohe Plattengeschwindigkeit zurückgeführt, da dadurch ein Lithosphärenelement nur eine relativ kurze Zeit über der Wärmequelle liegt.
Nachdem die Theorie der Plattentektonik etabliert war, lag es nahe, unter der sich mit ca. 10 cm pro Jahr gegenwärtig nach Westnordwesten bewegenden pazifischen Platte eine relativ zu dieser ruhende Quelle thermischer Energie anzunehmen, die eben diese Hot-Spot-Spuren dann an der Oberfläche "einbrennt". Inzwischen, und das hat auch obige Klassifizierung gezeigt, weiß man, daß es auch viele Mantel-Plume-Hot-Spots, die auf Steady-state-Plumes zurückzuführen sind, ohne solche Spuren gibt. Dadurch blieb dort der Zusammenhang zu Mantel-Plume-Strukturen eher verborgen.
Die Hawaii-Vulkane weisen vier vulkanische Abfolgen auf, die sich in verschiedenen Kompositionen der Laven und der Xenolithe zeigen (ten Brink und Brocher, 1987):
1. Zu Beginn erfolgen submarine Eruptionen alkalischer und
tholeiitischer Basalte.
2. Danach kommt es zum Aufbau tholeiitscher Schildvulkane.
3. a. Im Anschluß an den Kollaps der gebildeten Caldera, wobei
der Schild mit Alkalibasalten gekrönt wird, findet
b. eine Periode der Ruhe und Erosion statt.
4. Nach der Erosionsphase gibt es Eruptionen alkalischer Basalte,
Basanite, Nephelinite und Melilithe.
Dabei differieren die Xenolithe bei jeder Eruptionsphase. Dies kann an der Tiefe der Ursache und oder der Magmakammer liegen.
Nach Jackson et al. (1972) dauert die Vulkanaufbauphase in der Regel nicht länger als ca. 0,5 bis 1,5 Millionen Jahre. Da nach Walcott (1970b) auf Kontinenten isostatische Ausgleichsbewegungen sich innerhalb von Zeiträumen einer Dimension von tausend bis zehntausend Jahren abspielen und es darüberhinaus keinen Grund gibt, daß dies auf ozeanischer Kruste anders ist, sollte ein Vulkangebäude praktisch kurz nach seiner Entstehung kompensiert sein. Nach Walcott (1970a) führt die vulkanische Auflast zu einer Beanspruchung der Lithosphäre gemäß Abb. 54c in Kap. 7.1.. Danach drückt der Vulkanbau die Lithosphäre unter seinem Gewicht ein. Dadurch kommt es zu Eindellungen um die Vulkane herum. Etwas weiter weg kommt es jedoch zu Anhebungen. Ob hierin die alleinige Ursache für eine Schwellenbildung gesehen werden kann, behandeln die Kap. 5.4. und 7.1..
Geophysikalische Untersuchungen der Krustenstruktur unter Hawaii begannen mit den Ergebnissen der Schweremessungen von Vening Meinesz (1941) und Woollard (1951). Die Strukturen des Vulkaninneren und der umgebenden ozeanischen Kruste wurden aus refraktionsseismischen Messungen abgeleitet (Hill, 1969; Zucca und Hill, 1980; Zucca et al., 1982; Hill und Zucca, 1987). Diese Autoren fanden die Moho in 18,5 km unter NN unter Mauna Loa und 16 km unter Kilauea. Alle seismischen und Dichtemodelle zeigen eine deutliche verdickte Kruste unter den Inseln, können aber durch die unbekannte Dichteverteilung in den oberflächennahen Schichten verfälscht sein. Ellsworth und Koyanagi (1977) entwickelten ein Modell, das dreidimensional die Geschwindigkeitsstruktur bis zu 65 km Tiefe unter der Insel Hawaii zeigt. Die Moho weist einen Geschwindigkeitssprung von 0,9 km/s und einen Dichtekontrast von 0,4 g/cm3 auf (Lindwall,1988). Die tiefere Krustenstruktur leiteten Watts et al. (1985) aus dem Studium der Biegeeigenschaften der Kruste ab.
Ein Merkmal der Hawaii-Inseln ist ihre Absenkung mit dem Alter. Dies liegt an der Plattenbewegung. Die Migrationsrate liegt bei etwa 9,3 cm/Jahr (LeMasurier und Rex, 1989; Clague und Dalrymple, 1987; McDougall, 1979). Je mehr sich die Lithosphäre vom Mantel Plume entfernt, desto mehr kühlt sie ab. Sie verdickt sich und erreicht normale Mächtigkeiten. Dadurch sinkt sie ein, was wiederum ein Einsinken der auf ihr aufgebauten Vulkaninseln zur Folge hat ("island subsidence" nach Crough (1978)).
5.2. Bathymetrie, Geoid und Freiluftschwere
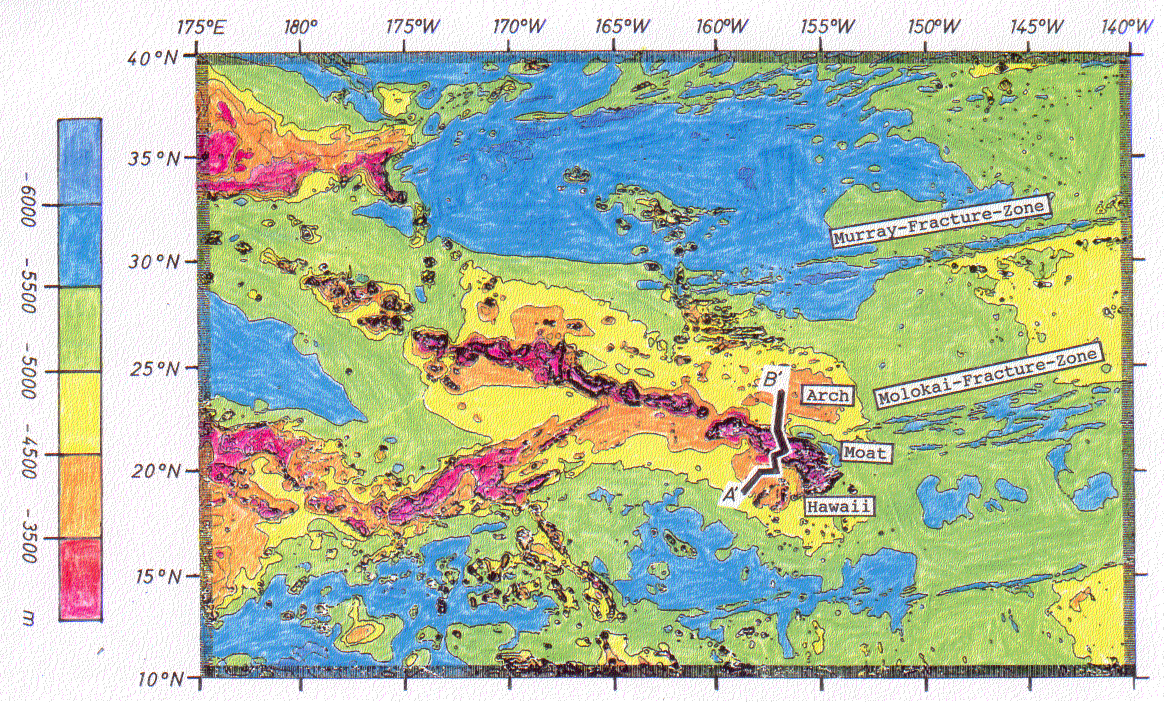
Das in Abb. 33 gezeigte Gebiet im nördlichen Pazifischen Ozean enthält den regionalen Bereich um den Hawaii-Hot-Spot. Die bathymetrischen Strukturen, die dieses Gebiet beherrschen, sind die langgestreckten, in Ost-West-Richtung verlaufenden, sich durch tieferes Wasser hervorhebenden Transformstörungen im Osten des Gebietes und die vielen sich ellipsenförmig bei der Darstellung der Bathymetrie abzeichnenden Seamounts, die entweder isoliert oder linienhaft zu Gruppen vereinigt stehen. Die Seamounts mit der größten Amplitude und Wellenlänge gruppieren sich längs einer in Ostsüdost-Westnordwest-Richtung durch das Gebiet verlaufenden Struktur. Am östlichen Ende dieser Struktur liegt der Archipel der Hawaii-Inseln. Nach Westnordwest nimmt die Amplitude der Seamounts allmählich ab. Die gesamte Struktur umfaßt die Insel- und Seamountkette der Hawaii- und Midway-Inseln. Bei genauerem Hinsehen auf Abb. 33 erkennt man, daß die Inselkette von einer regionalen Aufdomung, durch flacheres Wasser gekennzeichnet, umgeben ist. Diese Schwellung wird durch den Verlauf

Abb. 33.
Bathymetrie der Hawaii-Schwelle. Der Isolinienabstand beträgt
500m, die 5000m-Tiefenlinie (Abgrenzung zwischen grüner und
gelber Signatur) markiert den Bereich der Hawaii-Schwelle.
Sämtliche flacheren Gebiete mit Seamountketten sind rötlich
ausgewiesen. Die Hawaii-Kette ist jedoch durch die dortige enge
Lage der Isolinien klar dominant. Eingetragen ist die Lage des
den Abb. 38 und Abb. 39 zugrundeliegenden Profils A'B'. Weiter-
hin gekennzeichnet sind die Molokai- und die Murray-Fracture-
Zone sowie Senken um die Inseln im Nahbereich ("Moat") und Auf-
wölbungen in weiterer Entfernung der Inseln ("Arch"), vgl. Kap.
5.3.1. Die Daten entstammen dem "ETOP-5" Data Set des geophysi-
kalischen Datenzentrums in Boulder, Colorado, USA.
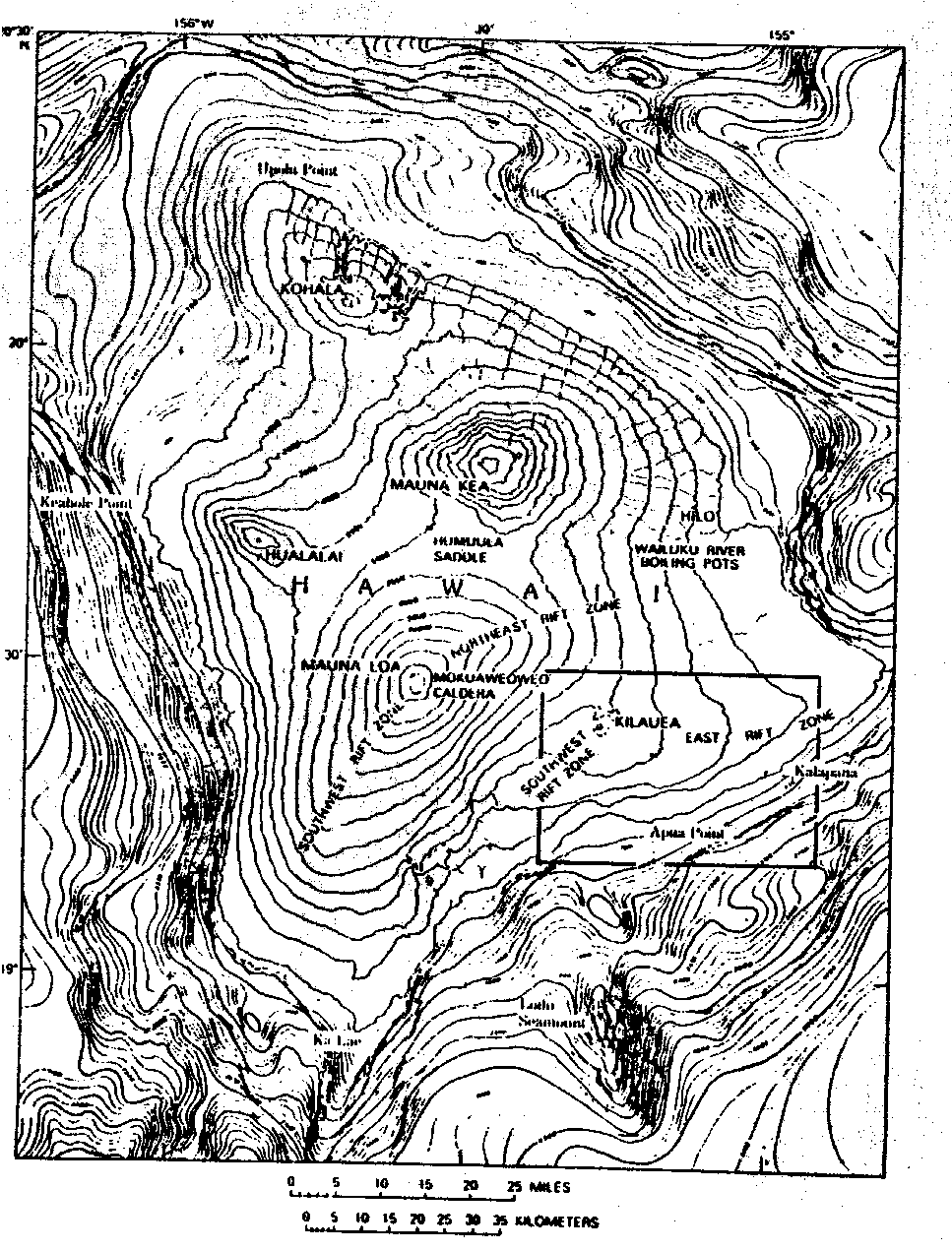
Abb. 34. Topographie bzw. Bathymetrie des zentralen Bereichs des Hawaii-
Hot-Spots. Dargestellt ist die Insel Hawaii (Big Island) sowie
die derzeit aktiven Vulkane des Hawaii-Hot-Spot: Loihi Sea-
mount, Kilauea und Mauna Loa. Aus Ryan (1988).
der -5000m - Isolinie markiert. Danach befinden sich die Hawaii-Inseln unmittelbar am "Kopf" (dem östlichen Ende) der Schwelle. Nach Westen hin umrahmt die Schwelle zunächst die Seamount-Kette in gleichbleibendem Abstand, bevor sie sich verjüngt und ausläuft.
Die Schwelle wird auf sublithosphärische Ursachen zurückgeführt. Auffällig ist ferner, daß diese Schwelle sich nicht östlich der Inseln ausdehnt. Vielmehr endet sie recht abrupt mit der Lage von Big Island. Außerdem ist eine nördlich und südlich der Kette liegende leichte Verflachung zu erkennen. Unmittelbar um die Inseln herum ist das Meer tiefer. Die Verflachung wird auch als "Arch" und die Senke als "Moat" bezeichnet (Watts et al., 1985). Dies kann offenbar auf die Vulkanauflast (Durchbiegung der Kruste) zurückgeführt werden.
Abb. 34 zeigt das gegenwärtige, aktive Zentrum des Hawaii-Mantel-Plume-Hot-Spots. Hier erkennt man, daß sich der Vulkanismus weiter nach Osten ausbreitet, während er im Westen erlöscht. Dabei konzentriert sich die Aktivität zur Zeit auf Kilauea und Loihi Seamount. Loihi ist der jüngste bekannte Vulkanbau der Hawaii-Kette. Die Darstellung des Geoids nach Abb. 35 entspricht der Darstellung der Geoidanomalien, die man nach der Subtraktion eines sphärisch harmonischen Referenzfeldes vom Grad und der Ordnung < 10 unter Benutzung der Koeffizienten von Rapp (1981) vom Geoid nach Marsh et al. (1986) erhält. Die Geoidhöhen von Marsh et al. (1986) beziehen sich auf das "1980 International Union of Geodesy and Geophysics (IUGG)"- Ellipsoid (Moritz, 1980). Die Problematik einer sinnvollen Geoiddarstellung diskutieren in diesem Zusammenhang McNutt und Shure (1986) und Sleep (1990).
Das Geoid wird im wesentlichen durch die Oberflächenstruktur geprägt. In der Darstellung von Abb. 35 werden Strukturen, die im Wellenlängenbereich von etwa 400 km bis 4000 km liegen, betont. So sind einerseits die kurzwelligeren "Tiefseesenken" , die z. B. Wellenlängen von einigen hundert Kilometern aufweisen, und die Hawaii-Kette deutlich zu erkennen. Andererseits sind aber auch langwelligere Elemente wie beispielweise das Geoid-Hoch nordöstlich der Hawaii-Inseln in den Daten zu finden. Im Bereich des Pazifiks um die Hawaii-Inseln befinden sich mehrere Hochs und Tiefs, deren Betrag bei einigen Metern Geoidanomalie liegt. Diese regionalen Hochs und Tiefs weisen Wellenlängen von einigen tausend Kilometern auf. Sie befinden sich im offenen Pazifischen Ozean und sind nicht mit markanten bathymetrischen Merkmalen korrelierbar. Dies gilt insbesondere für das Tief südöstlich der Hawaii-Inseln und das Hoch nordöstlich dieses Archipels. Bemerkenswert ist die Geoidstruktur um die Hawaii-Inseln herum. Hier liegt ein regionales Hoch mit einer Amplitude von ca. 5m und einer Wellenlänge von ca. 1500 km in Nordsüdrichtung. Die Struktur dieses Hochs ist jedoch nicht vergleichbar mit den Hochs der Umgebung. Vielmehr ist dieses regionale Hoch überprägt von der Geoidstruktur in unmittelbarer Inselnähe selbst. Insbesondere nördlich der Inseln liegt ein Keil leichter Absenkung vor, die Inseln selbst stellen eine sehr große lokale Geoidanomalie dar. Das Geoid der Hawaii-Kette ist durch die Auflast der Vulkangebäude geprägt.
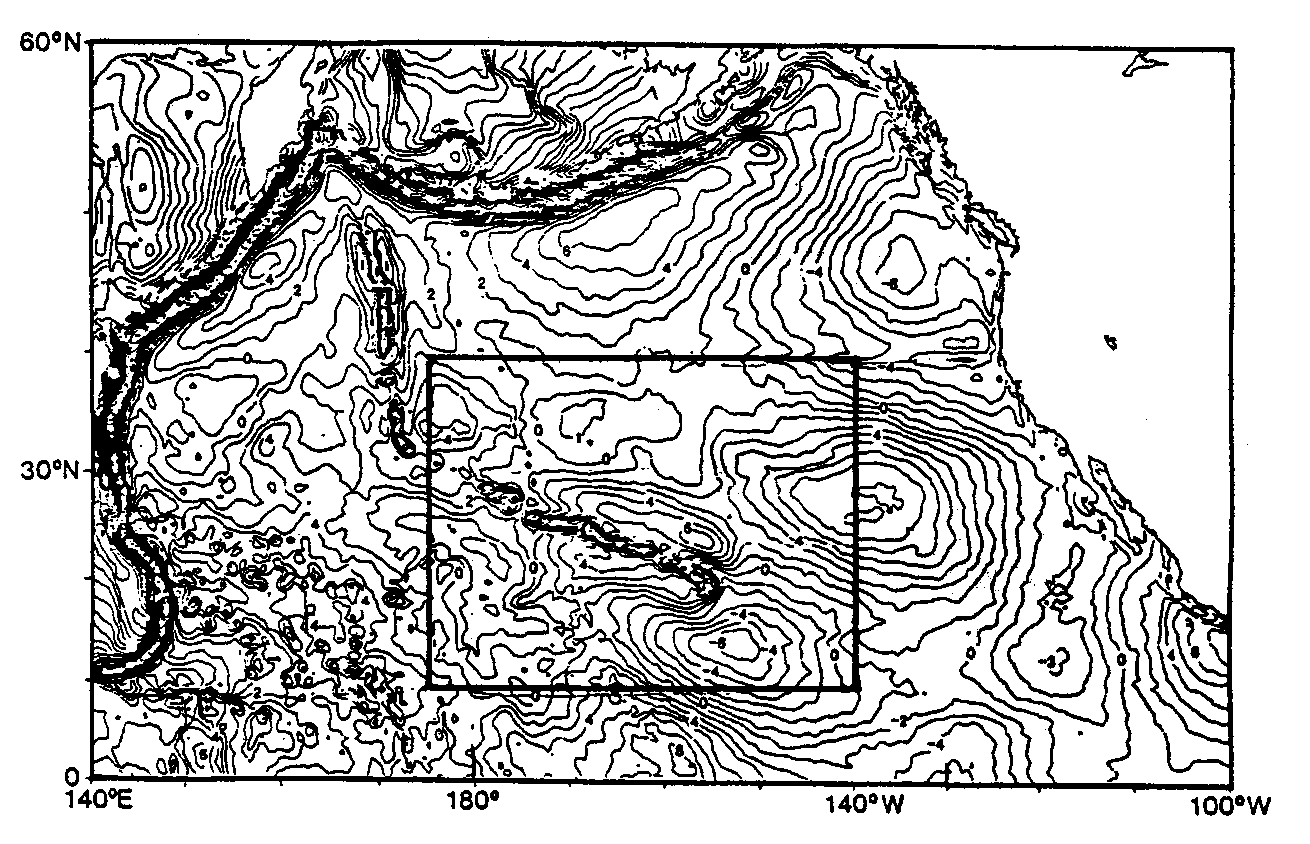
Abb. 35. Geoidsignal des Nordpazifiks nach Sleep (1990). Die beobachte-
te, gefilterte Geoidhöhe wurde berechnet unter Ausschluß der
sphärischen harmonischen Koeffizienten kleiner als Grad 11 und
größer als Grad 101 (Sandwell und Renkin, 1988). Damit werden
Strukturen, die Wellenlängen von einigen hundert bis zu einigen
tausend Kilometern aufweisen, betont. Das Untersuchungsgebiet,
für das die 3D-Modellierung durchgeführt wird, zeigt der einge-
rahmte Teil (Kasten) um die Hawaii-Schwelle.
Neben den Daten der Bathymetrie und des Geoids zeigt auch die Freiluftschwere ein regionales Hoch um die Hawaii-Inseln herum (vgl. Abb. 36). Dieses Hoch ist nahezu identisch mit der Ausdehnung der Schwelle, markiert durch die 5000m-Tiefenlinie. Die Verwandtschaft der Datensätze Schwere, Geoid und Bathymetrie wird weiterhin deutlich bei Betrachtung der Situation in unmittelbarer Umgebung der Inseln. Dort zeigt auch die Freiluftschwere ein ausgeprägtes, dem allgemeinen regionalen Hoch überlagertes Schwereminimum um die Inseln herum. Die Inseln selbst weisen ein ausgeprägtes Maximum auf.
Nach Detrick und Crough (1978) indiziert die regionale Schwereanomalie über der Hawaii-Schwelle eine durchschnittliche Kompensationstiefe in der unteren Hälfte der Lithosphäre (in Tiefen von etwa 50 km bis zu 100 km) und nicht in der Asthenosphäre, was zu erwarten wäre, falls die Schwelle durch asthenosphärisches Fließen unterstützt würde. Dagegen schließt Watts (1976) aus den gleichen Daten, die Detrick und Crough (1978) verwendeten, durch die Annahme einer etwas anderen Schwellenform als Detrick und Crough (1978) auf eine Kompensationstiefe im Bereich der Basis der Lithosphäre oder sogar noch darunter. Während die Kompensationsmasse in größeren Tiefen (50 km bis 100 km) liegt, sieht es danach aus, daß die meisten Dichteveränderungen in der oberen Lithosphäre, also in Tiefenbereichen von weniger als 50 km, liegen (Detrick und Crough, 1978). Dies bestätigen auch die isostatischen Betrachtungen mittels der Massensummation nach Janle (1973), die in Kap. 9.2. vorgestellt werden. Die Hawaii-Schwelle entstand nach Detrick und Crough (1978) durch das Ausdünnen der Lithosphäre über dem Mantel Plume. Die Anwendung linearer Filter auf die Topographieresiduen und die Geoiddaten der Region um die Hawaii-Inseln liefert nach McNutt und Shure (1986) eine Kompensationstiefe von 70 km innerhalb der unteren Lithosphäre.
Bei "thermischen" Modellen liegen die kompensierenden Dichteanomalien in der unteren Lithosphäre (siehe z. B. Crough (1978) oder Liu und Chase (1989)). Bei "dynamischen" Modellen befinden sich die kompensierenden Dichteanomalien unterhalb der Lithosphäre (siehe z. B. Courtney und White (1986) oder Monnereau et al. (1993)). Ribe und Christensen (1994) kommen ebenfalls zu dem Schluß, daß die Kompensation im sublithosphärischen Bereich erfolgt.
Die Schlußfolgerungen dieses Absatzes entstammen der zitierten Literatur. An dieser Stelle muß der Autor anmerken, daß solche Interpretationen mit
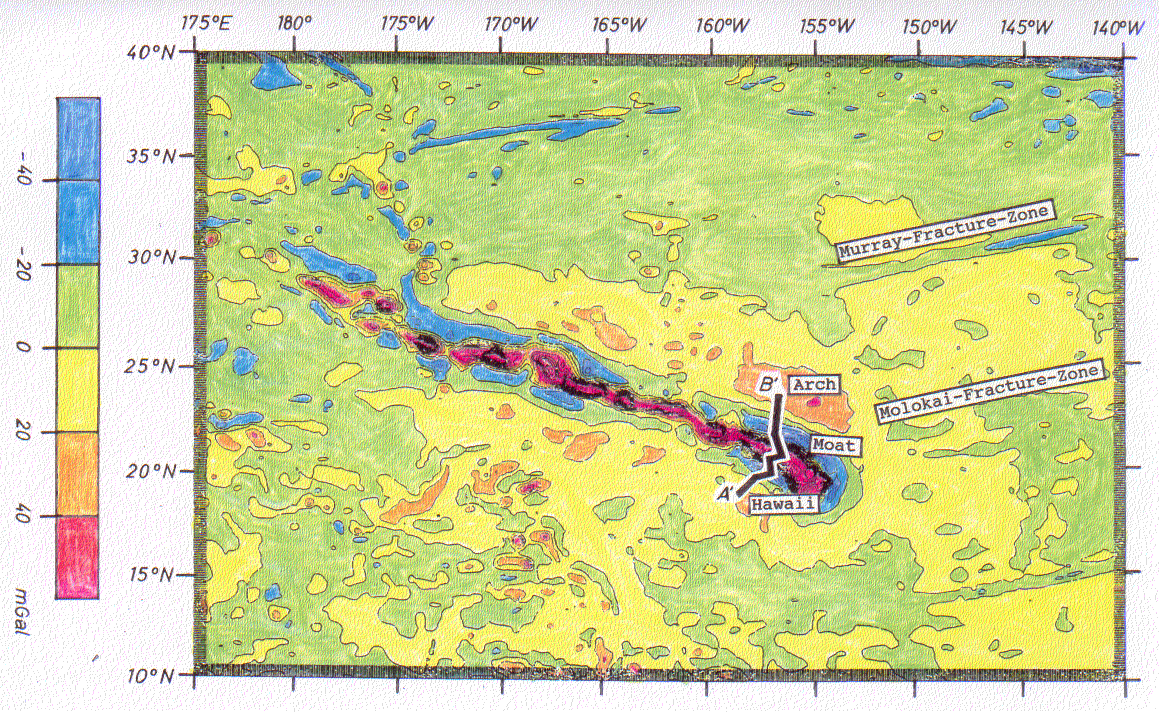
Abb. 36.
Freiluftschwere der Hawaii-Schwelle, abgeleitet aus SEASAT-Da-
ten. Der Isolinienabstand beträgt 20 mGal. Die Nullinie (Iso-
linie zwischen grüner und gelber Signatur) markiert hier zum
einen den regionalen Bereich der Schwelle und zum anderen einen
Bereich der Absenkung um die Inseln herum. Diese lokalen Minima
(tiefblaue Signatur) und die lokalen Maxima (orange Signatur im
Bereich der Schwelle und rote Signatur im Bereich der Seamount-
und Inselkette von Hawaii) treten besonders hervor. Eingetragen
ist die Lage des den Abb. 38 und Abb. 39 zugrundeliegenden Pro-
fils A'B'.
der Methode der Gravimetrie nicht ohne weiteres möglich sind. Dies illustriert die Abb. 44 in Kap. 5.4.2.. Daher müssen die Aussagen in diesem Absatz kritisch gesehen werden.
5.3. Zweidimensionale Krustenmodelle aus der Literatur
5.3.1. Die seismische Datengrundlage der 2D-Modelle
Das Lamont-Doherty Geological Observatory und das Hawaii Institute of Geophysics haben im Jahre 1982 eine seismische Meßkampagne, das Hawaii-Experiment, nahe Oahu (vgl. Abb. 37a) mit zwei Schiffen gestartet. Das Experiment bestand aus CDP- ("common depth point") Daten, COPs "constant offset profiles" und elf ESPs ("expanding spread profiles"), die entlang eines 600 km langen und 100 km breiten Profilnetzes quer zur Streichrichtung der Hawaii-Kette aufgenommen worden sind (Watts et al., 1985). Die Messungen dienten der Bestimmung von Randbedingungen für Modelle der Biegung der ozeanischen Kruste durch die vulkanische Auflast der Hawaii-Vulkankette. Dazu müssen die seismischen Geschwindigkeiten der verschiedenen Tiefen durch Refraktionsseismik bestimmt sowie die laterale Ausdehnung der Sedimente und der Krustenreflexionen mittels der Reflexionsseismik kartiert werden.
Zunächst werden in diesem Abschnitt weitere Informationen zur seismischen Datengrundlage gegeben. Anhand dieser werden dann die Krustenmächtigkeiten, die ermittelt worden sind, vorgestellt und diskutiert. Dabei wird auf den Kompensationsprozeß der Inselkette eingegangen.
Der Datensatz von ten Brink und Brocher (1987) beinhaltet zum einen Mehrkanalrefraktionsseismik (ESPs) zur Bestimmung von Geschwindigkeits-Tie-
a.
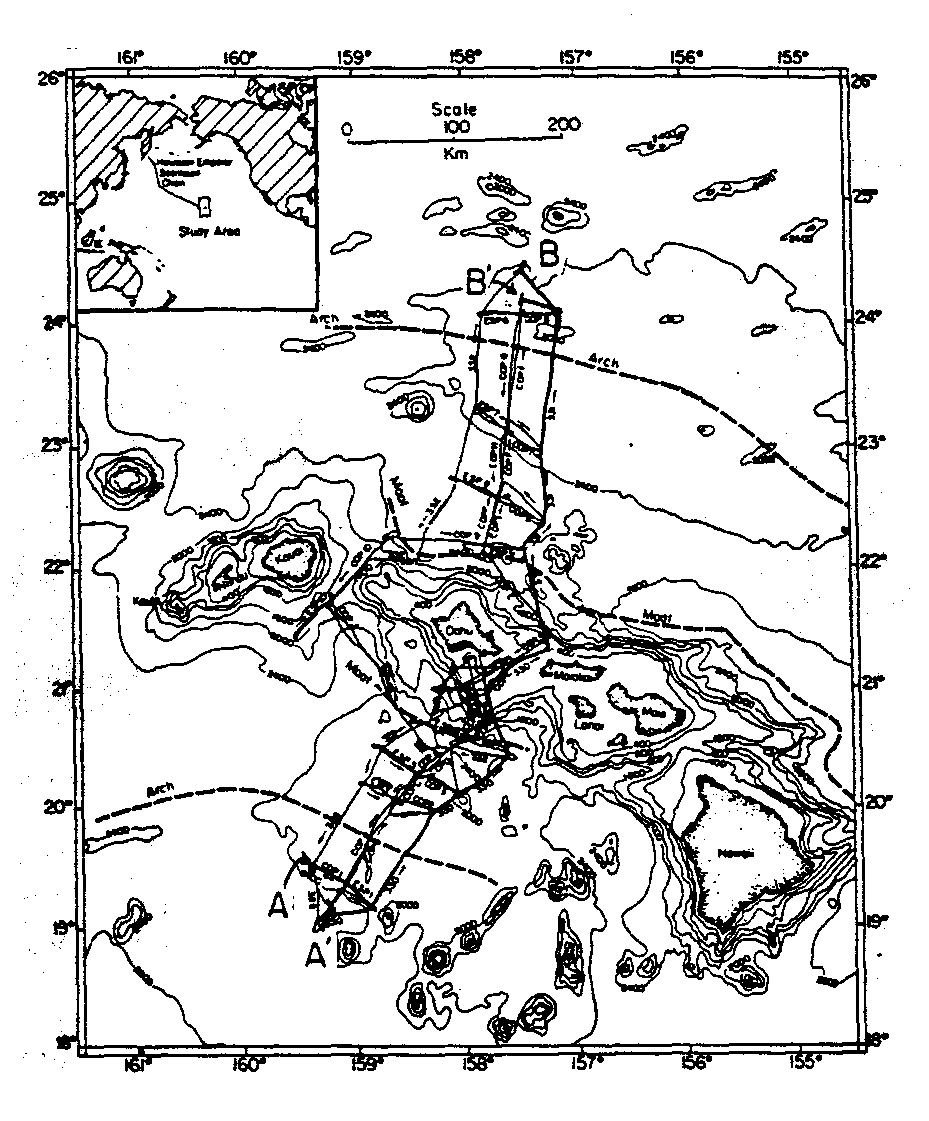
Abb. 37. a. Karte der Hawaii-Inseln mit Lage der Profile der seismischen
Meßkampagne. Die feinen Linien markieren die Lokationen ein-
zelner CDP, COP und ESPs. Die dicke Linie ist die Lokation
von ESP1/COP1 und CDP330/331, vgl. b., bzw. das Profil AB.
(Watts et al., 1985).
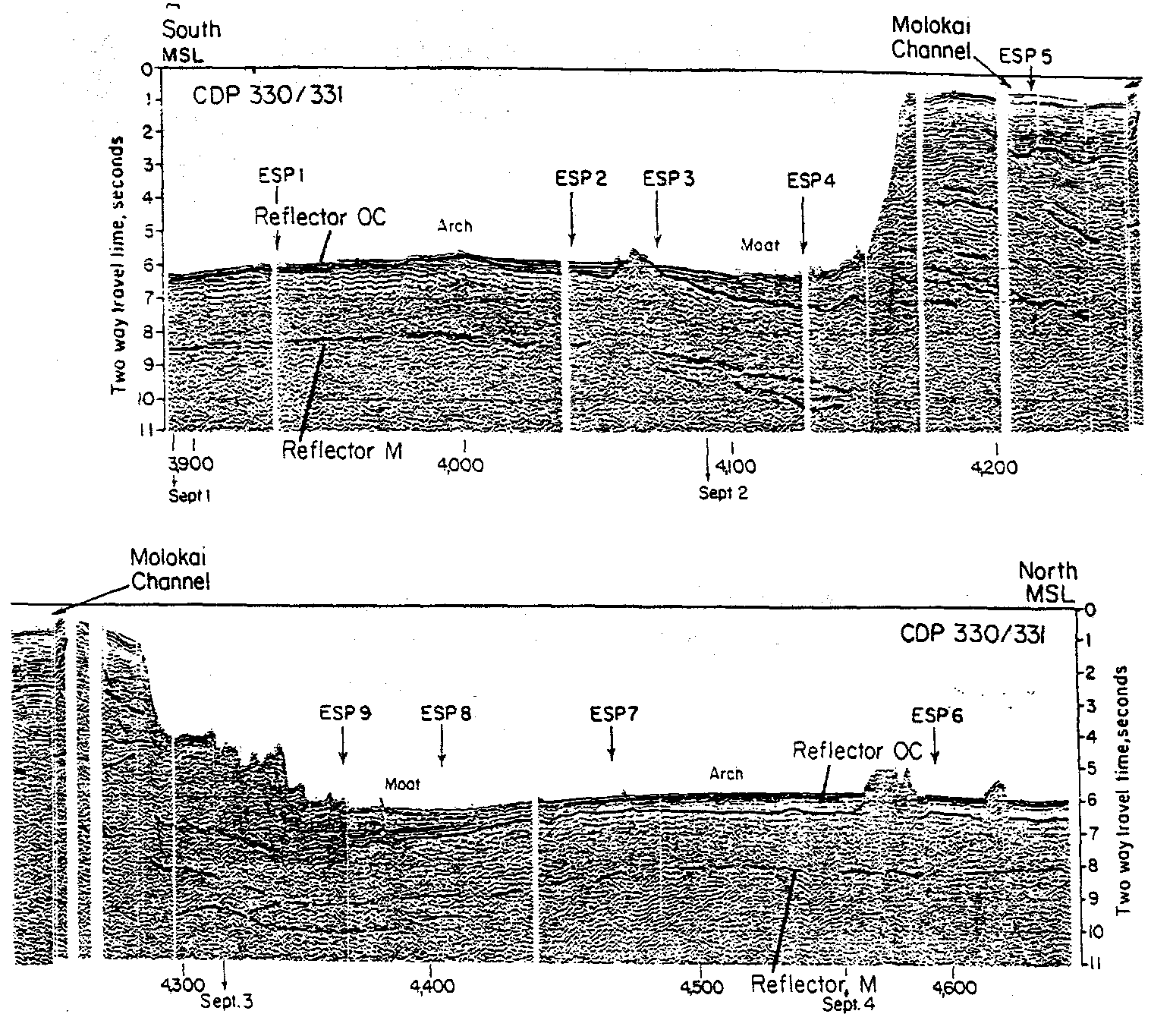
b. Reflexionsseismische Sektion längs des Profiles AB (CDP
330/331). Die schwarzen Eintragungen heben starke Reflekto-
ren hervor. Der bei etwa 8s liegende Reflektor M bezeichnet
die über etwa 50 km verfolgbare Krusten-Mantel-Grenze. Der
Reflektor OC bezeichnet das Grundgebirge. Die Zahlen unter-
halb der Sektion sind die vom Schiff zurückgelegten Entfer-
nungen.
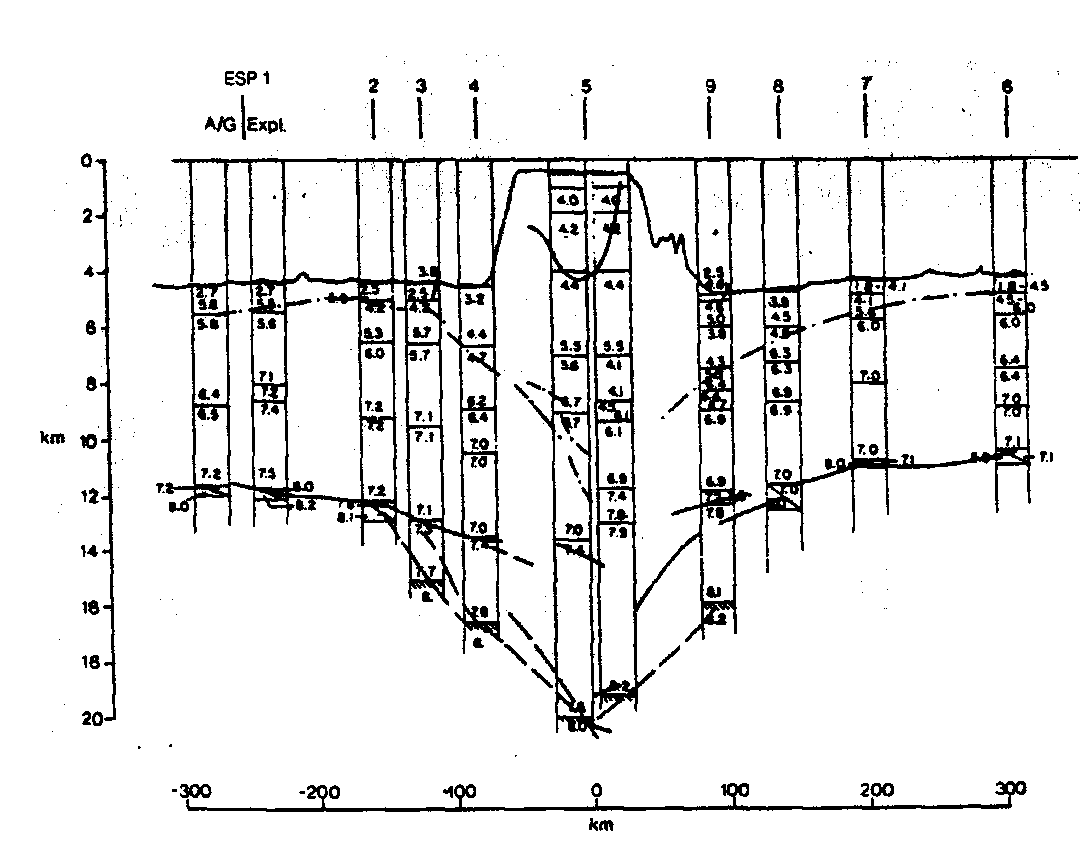
c. vP-Geschwindigkeits-Tiefen-Analyse für die ESPs 1-9, deren
geographische Lage in a. abgebildet ist. Bei einer horizon-
talen Linie findet eine größere Geschwindigkeitsänderung
statt. Die eingetragenen Zahlen bezeichnen die Geschwindig-
keiten in km/s. Eingetragen sind die Reflektoren aus b.,
welche mit Hilfe der Geschwindigkeiten aus der Zeitskala in
die Tiefenskala transformiert wurden (Watts et al., 1985).
b.
c.
fenverteilungen und zum anderen mit den Profilen der Refraktionsseismik zusammenfallende und sich kreuzende mehrkanalige Weitwinkel-Reflexionsseismik. Eine detaillierte Darstellung der Daten-Gewinnung und der Processing-Methoden kann bei Stoffa und Buhl (1979), Buhl et al. (1982) und bei NAT Study Group (1985) nachgelesen werden. Weitere Details zur Navigation und zu Korrekturen für das seismische Hawaii-Experiment sind in ten Brink (1986) dargestellt.
In Abb. 37 sind die wichtigsten seismischen Ergebnisse zusammengestellt. Nach Abb. 37b nimmt die Laufzeit zwischen Meeresboden und dem Reflektor M vom "Arch" (vgl. Abb. 37a) zum "Moat" (vgl. Abb. 37a) zu. Das deutet auf eine Verdickung der Kruste unter dem Moat (Senke um die Hawaii-Inseln herum) hin. Außerdem gibt es nach Abb. 37b Hinweise darauf, daß sich der Reflektor M unter dem Moat spaltet (Watts et al., 1985). Weder dies noch die Krustenverdickung sieht dagegen Lindwall (1988). Die Ansichten von Watts et al. (1985), die im übrigen auch von ten Brink und Brocher (1987) vertreten werden, und Lindwall (1988) werden in Kapitel 5.3.2. weiter betrachtet.
Die Geschwindigkeits-Tiefen-Funktion zeigt ein progressives Ansteigen von 2,5 km/s bis 8,1 km/s (Watts et al., 1985). Die Resultate aus den ESPs wurden auf das bathymetrische Profil A'B' (vgl. Abb. 37a) projiziert. Dieses Profil bildet auch die Grundlage für die in Kap. 5.3.2. betrachteten 2D-Dichtemodelle der Kruste. Aus Abb. 37c ist zu ersehen, daß die gesamte Krustendicke von etwa 6,5 - 6,8 km unter dem Arch und etwa 10,5 - 12,0 km unter dem Moat bis auf 18,0 - 19,0 km unter dem zentralen Bereich des hawaiianischen Rückens zunimmt. Watts et al. (1985) entwickelten die in Kap. 5.3.2. in Abb. 38 dargestellte Modellkruste für Hawaii unter Zuhilfenahme der Freiluftschwere. Die Abb. 38 zeigt die beiden von Watts et al. (1985) erarbeiteten alternativen Vorstellungen in der Variation der Struktur des subkrustalen Körpers. Im ersten Modell wird von einer verdünnten ozeanischen Kruste unter den Inseln ausgegangen, im zweiten Modell wird eine normale Mächtigkeit der Kruste angenommen. Zwischen diesen beiden Modellen können die Daten nicht unterscheiden.
5.3.2. Interpretation der 2D-Dichtemodellierung
Basierend auf einem Modell der Biegung einer elastischen Platte über einem nachgebenden Substratum unter einer Auflast von Vening Meinesz (1948) und Gunn (1943) haben Walcott (1970a,b), Watts und Cochran (1974), Watts (1978) und Kunze (1980) eine effektive Biegesteifigkeit der ozeanischen Platte von 5 . 1029 - 5 . 1030 dyn cm ermittelt, die einer elastischen Dicke Te = 17,8 - 38,3 km entspricht (Watts et al., 1985). Der Wert von Te hängt jedoch von der Art des zugrundegelegten Modells ab. Während Walcott (1970a,b) eine unter den Inseln gestörte Platte annimmt, gehen Cochran (1974), Watts (1978) und Kunze (1980) von einer geschlossenen Platte aus.
Die genaue Struktur der Moho ließ sich für den von Watts et al. (1985) eingeführten subkrustalen Intrusivkörper, vgl. Abb. 38, nicht aus den seismischen und gravimetrischen Daten ableiten. Im Modell A (vgl. Abb. 38) weist der subkrustale Körper eine Dichte von 3,15 g/cm3 auf. Die Kruste selbst ist ausgedünnt. In Modell B verkleinert sich der subkrustale Körper im oberen Bereich. Dieser wird durch die hier überall gleichmächtige, nicht ausgedünnte Kruste ersetzt. Damit liegt hier nunmehr anstatt der höheren Dichte des Intrusivkörpers nur die Dichte der Kruste, die Watts et al. (1985) mit 3,0 g/cm3 ansetzten. Die dadurch auftretende negative Dichtedifferenz von Modell A zu Modell B wird durch eine in den Intrusivkörper eingesetzte vulkanische Röhre mit der Manteldichte von 3,33 g/cm3 kompensiert.
Im Zusammenhang mit Rifting-Prozessen (Zusammenhänge zwischen Hot Spots und Rifting-Prozessen wurden bereits in Kap. 4.2. herausgestellt) sehen Meissner und Köpnick (1988) unter anomalen Plateaus und Strukturen im Randbereich des Atlantiks Körper an der Krustenbasis, die sich durch hohe vP-Geschwindigkeiten (7,2 - 7,8 km/s) auszeichnen. Nach Meissner und Köpnick (1988) fördern Zonen niederer Viskosität wie die der unteren kontinentalen Kruste eine massive laterale Ausbreitung von aufsteigendem Material. Als Konsequenz sehen Meissner und Köpnick (1988) eine laterale Intrusion von magmatischem Material in die untere kontinentale Kruste während der Zeit des initialen Riftings. Dieses Material führt nach Meissner und Köpnick (1988) später zur Bildung der durch hohe Geschwindigkeiten ausgezeichneten subkrustalen Intrusivkörper. Dieser im Zusammenhang mit Rifting-Prozessen abgeleitete Befund deckt sich mit dem von Watts et al. (1985), die die in Abb. 37c gezeigten hohen vP-Geschwindigkeiten in der Unterkruste von Hawaii ebenfalls als einen subkrustalen Intrusivkörper deuteten (vgl. Abb. 38).
Watts et al. (1985) geben für die effektive elastische Dicke der Lithosphäre Te einen Wert von Te = 25 km an, der im Falle einer nicht gebrochenen Platte auf etwa Te = 20 km hinausläuft. Obwohl der Wert von Te = 25 km als der beste für Hawaii erachtet wird, muß angemerkt werden, daß Te nach Watts (1978) eine strenge Funktion des Alters der Lithosphäre zum Zeitpunkt des Auftürmens der Vulkanlast ist. Nimmt man diesen Aspekt mit hinein, kommen Watts et al. (1985) auf einen Wert für die elastische Lithosphärendicke Te von Te = 30 - 40 km. Dieser Wert ist ungleich höher als der von Watts et al. (1985) als bester angenommener von Te = 25 km. Da allerdings nach z. B. Crough (1978) die Hawaii-Schwelle als Folge eines thermischen Auftriebs durch "reheating" der ozeanischen Lithosphäre durch einen Mantel Plume erklärt wird, wurde die 80 Millionen Jahre alte Lithosphäre von Hawaii thermisch auf ein Alter von etwa 30 Millionen Jahre zurückgestellt (nach Detrick und Crough, 1978). Damit ist der von Parsons und Sclater (1977) gegebene Zusammenhang zwischen dem Wärmefluß und dem Alter der Lithosphäre nicht mehr erfüllt (vgl. auch Kap. 2.2.2.2. Punkte (5) und (6)). Aus diesem Grunde muß für die Berechnung der effektiven elastischen Dicke Te ein Wert von 30 Millionen Jahre genommen werden, der dann auf einen Wert für Te von 18 - 23 km führt. Dies ist in guter Übereinstimmung mit dem Wert Te = 25 km. Ein Biegungsmodell mit dem Wert von Te = 25 km erklärt das generelle elastische Verhalten der Kruste um Oahu. Der Einfluß des subkrustalen Intrusivkörpers hingegen wird darin nicht mit aufgenommen.
Den Dichtemodellen aus Abb. 38 und Abb. 39 liegen die Ergebnisse refraktionsseismischer Messungen und Freiluftschweredaten zugrunde. Dabei haben Watts et al. (1985), ten Brink und Brocher (1987) und Lindwall (1988) die Umrechnung der seismischen vP-Geschwindigkeiten in Dichtewerte mit Hilfe der von Christensen und Salisbury (1975) sowie Manghnani und Woollard (1968) bereitgestellten Beziehungen durchgeführt. In beiden Modellen (Abb. 38 und Abb. 39) wurde der Vulkanbau mit den Dichten von 2,3 g/cm3, 2,5 g/cm3 sowie 2,7 g/cm3 und die Sedimente mit den Dichten 2,3 g/cm3 und 2,6 g/cm3 angesetzt. Lindwall (1988) teilt die Kruste ferner in die Dichten 2,95 g/cm3 sowie 3,0 g/cm3 ein. Watts et al. (1985) dagegen sehen eine einheitliche Kruste (in Abb. 38 dick hervorgehoben) von 3,0 g/cm3. Watts et al. (1985) legen eine klare Grenze für die Krusten-Mantel-Grenze fest. Lindwall (1988) nimmt dagegen einen Übergangsbereich an, den er mit einer Dichte von 3,15 g/cm3 gekennzeichnet hat. In beiden Modellen zeigt sich, daß die Kruste im Bereich des Profils südlich der Inselkette mächtiger als nördlich der Inselkette ist. Ob dieses Ergebnis von lokaler oder regionaler Bedeutung ist, kann jedoch nicht festgestellt werden.
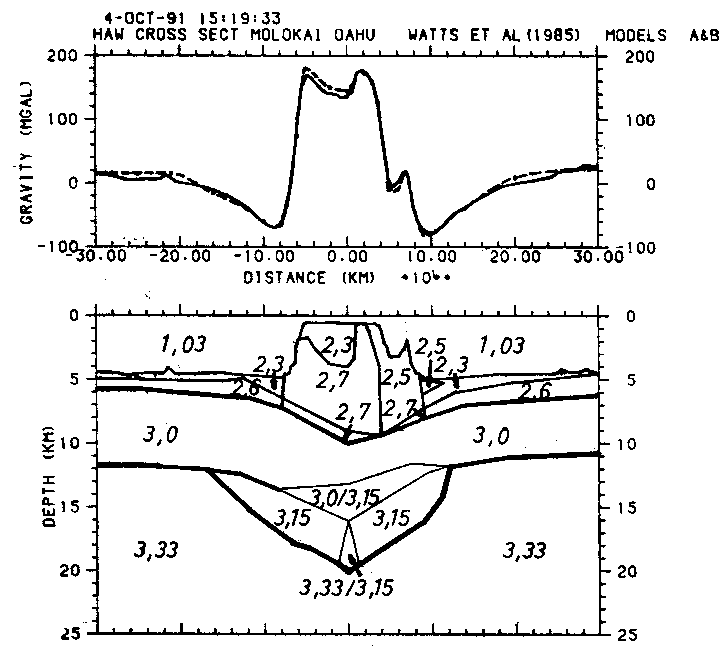 Abb. 38. Zweidimensionales Krustenmodell der Hawaii-Kette nach ten Brink
Abb. 38. Zweidimensionales Krustenmodell der Hawaii-Kette nach ten Brink
und Brocher (1987) sowie Watts et al. (1985). Die gestrichelte
Linie gibt die gemessene Freiluftschwere an. Das Modell besteht
aus einer auf die gleiche Modellschwere (durchgezogene Linie)
hinauslaufenden Version der Modelle A und B. Die Modelle A und
B unterscheiden sich durch die Form des subkrustalen Intrusiv-
körpers. In Modell A (erste Dichtewerte) liegt eine normale
Kruste vor, unter der im subkrustalen Körper eine dichtere zen-
trale Intrusion liegt. Im Modell B ist die Kruste ausgedünnt
und der subkrustale Körper weist eine einheitliche Dichte auf.
Alle Dichteangaben sind in g/cm
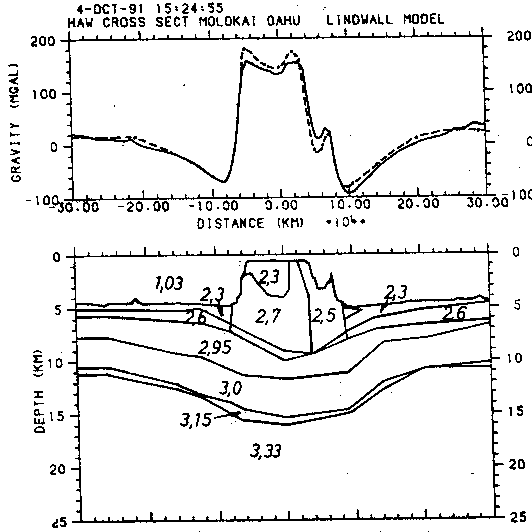 Abb. 39. Zweidimensionales Krustenmodell der Hawaii-Kette nach Lindwall
Abb. 39. Zweidimensionales Krustenmodell der Hawaii-Kette nach Lindwall
(1988). Lage des Profils vgl. Abb. 33, Abb. 36, Abb. 45 oder
Abb. 46.
Die seismischen Messungen sind nicht notwendigerweise auf dem in Abb. 36 gezeigten Profil eingefahren worden, obwohl das Modell die Struktur für dieses Profil darstellt. Vielmehr wurden dazu die refraktionsseismischen Ergebnisse von Watts et al. (1985) und Lindwall (1988) zu einem repräsentativen, die Hawaii-Kette schneidenden Profil zusammengefaßt (Projektion der ESPs auf das Profil A'B' in Abb. 37a). Dies stellt bereits eine Fehlerquelle in der Modellkonstruktion dar. Eine weitere Unsicherheit ist die bereits genannte unbekannte Dichteverteilung in den oberen Schichten. Ferner basieren die Modelle auf die von Christensen und Salisbury (1975) und Manghnani und Woollard (1968) angegebenen Geschwindigkeits-Dichte-Zusammenhänge. Solche Kurven betrachten in der Regel lediglich Labor- und nicht die in der Tiefe vorherrschenden (Druck- und Temperatur-) Bedingungen. Darstellungen der Abhängigkeit der vP- und vS-Geschwindigkeiten von der Temperatur befinden sich z. B. in Kern (1982). Danach verringern sich die Geschwindigkeiten bei zunehmender Temperatur. Somit verändern sich die Geschwindigkeits-Dichte-Beziehungen (eine Zusammenfassung der Geschwindigkeits-Dichte-Beziehungen ist in Gebrande (1982) gegeben) ebenfalls mit der Temperatur. Die vP- und vS-Geschwindigkeiten nehmen mit zunehmender Temperatur stärker ab als die Dichte. Dies wurde nur unzureichend berücksichtigt und geht daher ebenfalls zu Lasten einer eindeutigen Interpretation der Daten.
Die in den Abb. 38 und Abb. 39 gezeigten Dichtemodelle wurden mit einem vom Institut für Geophysik der CAU Kiel zur Verfügung gestellten 2D-Schweremodellierungsprogramm, welches auf dem Verfahren von Talwani et al. (1959) basiert, nachmodelliert. Das Modellieren verdeutlichte nochmals, daß die Modellschwere im wesentlichen von den oberflächennahen Gegebenheiten abhängig ist. Durch geeignete Änderungen, die noch mit den seismischen Ergebnissen kompatibel sind, lassen sich z.T. erheblich andere Dichteverteilungen nachmodellieren, ohne daß dabei die genauere Struktur in der Mohogegend eine größere Rolle spielt. Auf diese Weise ist es wohl auch zu erklären, weshalb die Autoren Watts et al. (1985) und Lindwall (1988) zu recht unterschiedlichen Ergebnissen kommen, obwohl die gleiche Datenbasis beiden zur Verfügung stand.
Die Modelle von Watts et al. (1985), Abb. 38, und Lindwall (1988), Abb. 39, unterscheiden sich im Bereich des Aufbaus der Krusten-Mantel-Grenze unter den Vulkanbauten. Watts et al. (1985) sehen hier Anzeichen für einen subkrustalen Körper. Dies sei dann ein Sill Komplex, der mit dem tholeiitischen Stadium des Hawaii-Vulkanismus assoziiert werden könne. Die Existenz dieses Körpers wird von Lindwall (1988) jedoch abgelehnt. Er sieht lediglich eine differenzierte Kruste, die unter der Vulkanauflast durchgebogen und damit verdickt ist. Beide Modelle vermögen die seismischen und Schweredaten hinreichend genau zu erklären, so daß hier keinerlei weitergehende Analyse möglich ist. Beide Modelle betrachten lediglich die Krustenstruktur in einer lokalen Umgebung. Um der Natur des Mantel-Plume-Hot-Spot-Vulkanismus auf die Spur zu kommen, muß auch der Sublithosphärenbereich in regionaler Ausdehnung mitbetrachtet werden. Die gezeigten Modelle der Abb. 38 und Abb. 39 mögen zwar den Aufbau der Kruste recht gut wiedergeben, sie sagen jedoch kaum etwas über die Hot-Spot-Natur der gesamten Struktur aus.
5.4. Der Mantel Plume als Ursache für die Hot-Spot-Tätigkeit
5.4.1. Mantel-Plume-Modelle aus Theorie und Labor
Die Idee von der Existenz des Mantel Plumes ist rein empirisch angesetzt. Bisher ist es nicht gelungen, die Existenz dieser Struktur zu beweisen. Lediglich die konstruierten Folgen, die in Kap. 2.2.1. gelisteten an der Oberfläche beobachtbaren Eigenschaften, sowie die tomographischen Ergebnisse aus Kap. 3.3.3. (Abb. 23) sind bekannt. Es gibt eine Vielzahl von Publikationen, die sich mit der Mantel-Plume-Struktur an sich auseinandersetzen. Sowohl Labormethoden als auch die numerische Mathematik werden angewendet, um zu Schlußfolgerungen über die Mantel-Plume-Struktur zu kommen. Die numerisch-theoretischen Verfahren gehen meist entweder dynamisch oder thermisch an das Problem heran.
Aus den experimentellen Laborergebnissen und den numerischen Rechnungen werden die verschiedenen Eigenschaften der Mantel Plumes abgeleitet. Dies betrifft deren Form und Größe, die Temperaturverteilung, deren Zusammensetzung, die Dichte und vieles mehr. Abb. 5 in Kap. 2.2.2. zeigt die klassische Form und Größe des Mantel Plumes, wie er aus verschiedenen Literaturquellen zu entnehmen ist.
Die Struktur der hypothetischen Mantel Plumes untersuchten u. a. Whitehead und Luther (1975), Olson und Singer (1985), Campbell et al. (1989) und Griffiths und Campbell (1990). Der Durchmesser eines Mantel Plumes kann mit ca. 1000 km angenommen werden (Griffiths und Campbell, 1991). Das pilzförmige Ausbreiten des asthenosphärischen Materials geschieht in einer Tiefe, die die Hälfte des Durchmessers ist. Das Ausbreiten ist zu Beginn des Mantel-Plume-Aufstiegs schnell, der Geschwindigkeitsabfall dieses Prozesses liegt bei t-3/4, wobei t die Zeit ist, die seit dem Beginn des Ausbreitungsvorganges verstrichen ist. Aufgrund der Größe der Mantel Plumes kommt als Ursprungsort die Kern-Mantel-Grenze in Frage. Die Mächtigkeit der Plume-Scheibe (Pilzhut) liegt bei ca. 200 km (Griffiths und Campbell, 1991). Nach Whitehead und Luther (1975) und Olson und Singer (1985) weist ein Mantel Plume, der pristinen Mantel durchstößt, einen pilzförmigen Hut mit einer sehr dünnen Aufstiegszone auf. Die dünne Aufstiegszone fordern neben den in Abb. 40c dargestellten Fällen auch Davies (1988), Richards et al. (1988) und Sleep (1987a,b). Das an der Oberfläche durch Mantel-Plume-Strukturen beeinträchtigte Gebiet umfaßt nach White und McKenzie (1989) eine Region mit einem Radius von bis zu 1000 km.
Courtney und White (1986) haben ihr Plume-Modell (Abb. 40b) anhand des Kapverden-Mantel-Plume-Hot-Spots erarbeitet. Dabei haben die Autoren die Dichtedifferenz des Mantel Plumes gegenüber der Umgebung durch thermische Prozesse modelliert. Danach ist der Mantel Plume in seinem Innern um mehrere 100 Grad Kelvin heißer als an seinen Randbereichen. Dies hat dann auch Auswirkungen auf die Dichteverteilung innerhalb des Mantel Plumes. Im Gegensatz zu Whitehead und Luther (1975), Olson und Singer (1985) oder Sleep (1987a,b) sehen Courtney und White (1986) oder Wyllie (1988) nicht einen sehr engen Aufstiegskanal, sondern einen weit mehr als 100km Durchmesser aufweisenden Aufstiegskanal asthenosphärischen Materials (vgl. Abb. 40b). Hier konzentrieren sich die heißen Zonen im Plume nur auf den zentralen Bereich der Aufstiegszone. Bei Wyllie (1988) fallen die noch bei Courtney und White (1986) als heiß betrachteten Gebiete in der sublithosphärischen Pilzstruktur heraus.
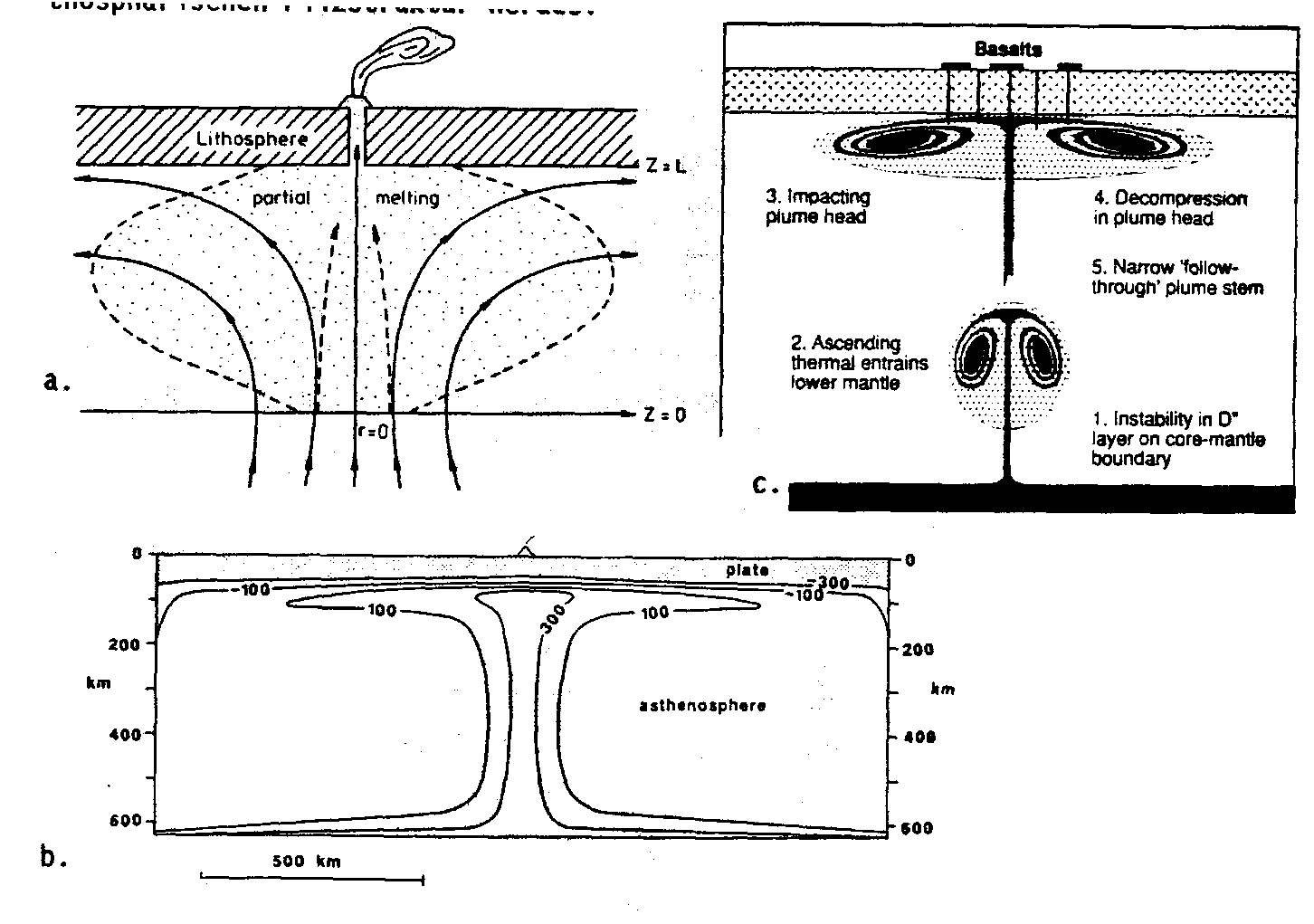
a.c.
b.
Abb. 40. Plume-Strukturen nach a) Li und Spohn (1991), b) Courtney und
White (1986) und c) Campbell und Griffiths (1990); Griffiths
und Campbell (1990); Richards et al. (1989).
Li und Spohn (1991) sehen in der Plume-Struktur ein Zwei-Phasen-System (Abb. 40a). Danach existieren partielle Schmelzen, deren Anteil am Gesamtplumevolumen an der Oberseite zunehmen. Damit liegt dort der Bereich verminderter Dichte und höherer Wärme. Die Dicke des Pilzkopfes geben Li und Spohn (1991) jedoch im Gegensatz zu Griffiths und Campbell (1991), die die Dicke des Pilzhutes mit 200 km angeben, mit ca. 40 km an. Für die nachfolgende 3D-Modellierung wird eine Dicke des Pilzhutes von etwa 100 km angenommen. Dieser Wert stellt einen Mittelwert aus den Werten der Literatur dar und wird weiterhin durch die in Abb. 23a,b,c,d gezeigten tomographischen Ergebnisse unterstützt. Im Rahmen eines zeitlichen Ablaufs für die Entwicklung eines Mantel Plumes zeigt die Abb. 40c sowohl den engen Aufstiegskanal asthenosphärischen Materials, den bereits Whitehead und Luther (1975) sowie Olson und Singer (1985) erwarteten, als auch die mögliche Strömung innerhalb des Plumes.
Li Yinting et al. (1983) haben gezeigt, daß sich aufsteigendes Plume-Material in einer von einem Viskositätsgradienten charakterisierten Umgebung lateral ausbreitet. Dies wird durch Zonen niederer Viskosität wie die der Asthenosphäre noch gefördert. Auch die Entstehung des von Watts et al. (1985) geforderten subkrustalen Intrusivkörpers wurde in Kap. 5.3.2. mit Hilfe der Ergebnisse von Meissner und Köpnick (1988) durch Ausbreitungsvorgänge in der niederviskosen unteren Kruste erklärt. Aufgrund der hohen Viskosität der Lithosphäre kann das Plume-Material nicht in die Lithosphäre eindringen. Die damit verbundene Ausbreitung des Plume-Materials an der Lithosphärenbasis führt dazu, daß sich der Plume im wesentlichen im Sublithosphärenbereich befindet.
Für die Erstellung eines Dichtemodells für eine Mantel-Plume-Hot-Spot-Struktur benötigt man Dichtewerte für die Plume-Struktur. Mit Hilfe der in Kap. 5.3.2. angesprochenen Geschwindigkeits-Dichte-Beziehungen lassen sich Dichten zwar aus seismischen Untersuchungen ableiten. Jedoch spielt gerade im Plume-Bereich die unsichere Temperaturabhängigkeit solcher Beziehungen eine Rolle. Da hierüber keine verläßlichen Daten vorliegen, wird die Dichteinformation aus theoretischen Betrachtungen abgeleitet.
Bei einer Mantelviskosität von 1022 Poise geben Richards et al. (1989) für den Mantel Plume eine um 0,1 g/cm3 gegenüber dem umgebenden Mantelgestein reduzierte Dichte an. Dieser Dichtekontrast folgt aus thermischen Betrachtungen nach Richards et al. (1988). Danach beträgt der thermische Dichtekontrast von Mantel Plume zu umgebendem Mantel
= - 0 T, (1)
wobei 0 die mittlere Manteldichte,
T der Temperaturkontrast zwischen Mantel Plume und
umgebendem Mantel
und der thermische Expansionskoeffizient mit
= 3 . 10-5 /K.
Dabei gehen Richards et al. (1988) von einer Manteldichte von
= 5,14 g/cm3 und einem Temperaturkontrast von T = 800 K aus. Der daraus resultierende Wert von = -0,1 g/cm3 ist sehr hoch.
Bei Sleep et al. (1988) und Sleep (1990) beträgt der Dichtekontrast = -0,03 g/cm3. Dieser Wert liefert nach Gl. (1) eine äquivalente Temperaturdifferenz von T = 300 K bei einer angenommenen Manteldichte von = 3,3 g/cm3. Sleep (1990) führt weiter aus, daß die durchschnittliche Mantel-Plume-Mantel-Temperaturdifferenz mit T = 200 K angesetzt werden kann, wobei lokale Spitzenwerte von 310 K bis 260 K möglich sind. Dies würde dann auf einen Dichtekontrast von = -0,02 g/cm3 führen.
Li und Spohn (1991) ermitteln die Dichtewerte für Mantel Plumes nach
= s (1- ) + l , (2)
wobei s = 3,3 g/cm3 die Matrixdichte (Manteldichte),
der prozentuale Anteil an Schmelze ("Porosität"),
l
Der Dichtekontrast ergibt sich dann gemäß
= s - (3)
zu = -0,025 g/cm3 bei einer angenommenen "Porosität"
von = 0,05.
Nimmt man an, daß der Mantel Plume eine überall etwa gleichmäßig erhöhte Temperatur gegenüber dem umgebenden Mantel besitzt, so folgt aus diesen Ausführungen als sinnvoller Dichtekontrast ein Wert von = - 0,02 g/cm3.
In den soweit betrachteten Modellen aus der Literatur wird die Mantel-Plume-Struktur immer als zylindersymmetrisch angenommen. Dies geht von der Vorstellung zentralsymmetrischen thermischen Aufstiegs aus, der keinerlei Fremdeinflüssen ausgesetzt ist. Es mag Mantel-Plume-Hot-Spots geben, auf die diese Annahme gut zutrifft, z. B. die Kapverden. Aber zumindest für den bekanntesten aller Hot Spots, Hawaii, scheint dies eher fragwürdig. Hier zeigt die den Hot Spot umgebende Schwelle elliptischen, nach Westen auslaufenden Charakter. Außerdem bewegt sich hier die pazifische Platte mit etwa 10 cm/Jahr nach Westen. Daher ist anzunehmen, daß sich die Plumestruktur hier durch äußere Einflüsse, hervorgerufen durch die (Ursachen der) Plattenbewegung, elliptisch verformt hat. Diesen Ansatz findet man bei Sleep (1990) im Rahmen der Diskussion um die sogenannte "stagnation line" asthenosphärischen Materials. Sleep (1990) plaziert die "stagnation line" bei 350 km bis 450 km ostsüdöstlich von Loihi Seamount. Als anschaulicher Vergleich bieten sich wieder Vorgänge in der Atmosphäre an, in der man auch in Strömungsrichtung deformierte Plumes findet. Hier sind dies die Cumulonimben, wenn sie sich im Bereich einer ostwärts ziehenden Kaltfront bilden. Die Neigung eines Mantel Plumes kann jedoch nicht beliebig groß sein. So zeigen z.B. Whitehead (1982), Olson und Singer (1985) und Olson und Nam (1986), daß ein Mantel Plume in einzelne, aufeinanderfolgende Tropfen zerfällt, wenn dieser mehr als 30 Grad geneigt ist. Einzelne Tropfen könnten möglicherweise Schübe von Hot-Spot-Aktivität längs mancher Inselketten erklären.
Der Mantel-Plume-Tätigkeit wird zumindest die initiale Schwellenbildung über dem Mantel-Plume-Hot-Spot zugeschrieben. Dabei gibt es Modelle, die die Schwellenbildung mit Vulkanismus unmittelbar als Folge des diapirischen Aufstiegs des asthenosphärischen Materials sehen. Andere Modelle hingegen betrachten auch die lithosphärische Wechselwirkung mit dem Mantel Plume, die dann erst zur Schwellenbildung mit Vulkanismus führt. Darauf wird später bei der Diskussion der Schwellenbildung in Kap. 7.1. näher eingegangen.
5.4.2. Schwerewirkung der Mantel-Plume-Struktur
Eine Aufgabe der vorliegenden Arbeit ist es, eine bessere physikalische Evidenz für die bislang rein hypothetisch angenommene Mantel-Plume-Struktur unter Hot Spots zu gewinnen. Neben der refraktionsseismischen Naherkundung (siehe oben) gibt es noch seismisch-tomographische Studien, die auf eine Mantel-Plume-artige Struktur hindeuten (vgl. Abb. 23 in Kap. 3.3.3.). Die Dichtemodelle für die Kruste des Hawaii-Mantel-Plume-Hot-Spots nach Watts et al. (1985) und Lindwall (1988) beachten nicht die Mantel-Plume-Struktur. Abb. 41 zeigt die Schwere- und Geoidwirkung eines zweidimensionalen, hypothetischen Hot-Spot-Modells mit einer Mantel-Plume-Struktur in der Sublithosphäre. Dabei wird deutlich, daß sich der Mantel Plume, sofern er existiert, in jedem Falle im Schwere- und Geoidsignal bemerkbar macht. Der Mantel Plume (Sublithosphärenpilz) zeigt nach Abb. 41 eine langwellige Schwereanomalie, die bei der Modellierung von Hot-Spot-Strukturen berücksichtigt werden muß.
Es sind verschiedene Faktoren, die die Schwerewirkung eines Mantel Plumes an der Oberfläche ausmachen. Vorstellbar sind
1. Mantel Plumes mit dicken Aufströmungszonen nach Wyllie (1988),
2. Mantel Plumes mit dünnen Aufströmungszonen nach Olson und
Singer (1985),
3. Mantel Plumes, die in der Größe variieren,
4. Mantel Plumes, deren Formen von zentralsymmetrisch über exzentrisch
bishin zu in Tropfen (Blobs) zerrissenen Strukturen reichen,
5. Mantel Plumes, die gegenüber dem umgebenden Mantel eine konstante
Temperatur- und damit Dichtedifferenz aufweisen und solche, die im
Innern verschiedenartige Temperaturgradienten aufweisen,
6. die Größe des Dichteunterschiedes Mantel-Plume-Mantel,
7. Mantel Plumes verschiedener Tiefenlagen unter der Oberfläche.
Als nächster Schritt wird vom 2D-Modell (Abb. 41) zum 3D-Modell übergegangen. Der wesentliche Unterschied besteht darin, daß der Mantel Plume sich im 3D-Fall nicht mehr unendlich senkrecht zum Profil ausdehnt. Damit vermindert sich der Schwerebeitrag der Struktur. In den nachfolgenden Abbildungen wurde die Mantel-Plume-Struktur zentralsymmetrisch angenommen.
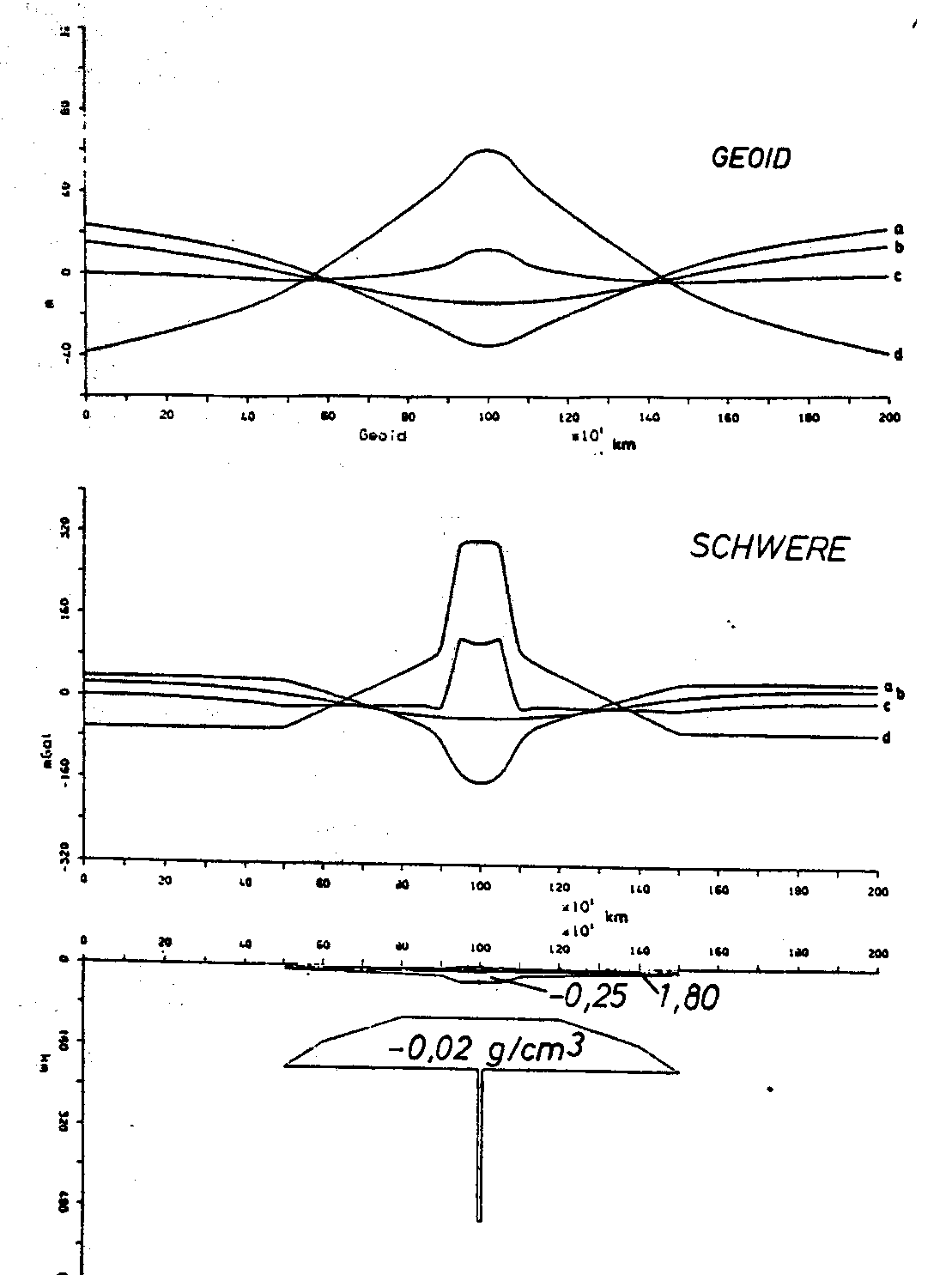
Abb. 41. Schwere- und Geoidwirkung eines zweidimensionalen, hypotheti-
schen Hot-Spot-Modells. Eine ozeanische Schwelle mit einer im
Scheitel aufliegenden Inselkette bildet das topographische Mo-
dell. Die Topographie ist zu 62,5 % Airy-isostatisch kompen-
siert. Im Sublithosphärenbereich liegt eine pilzhutförmige
Struktur mit einer um 0,02 g/cm
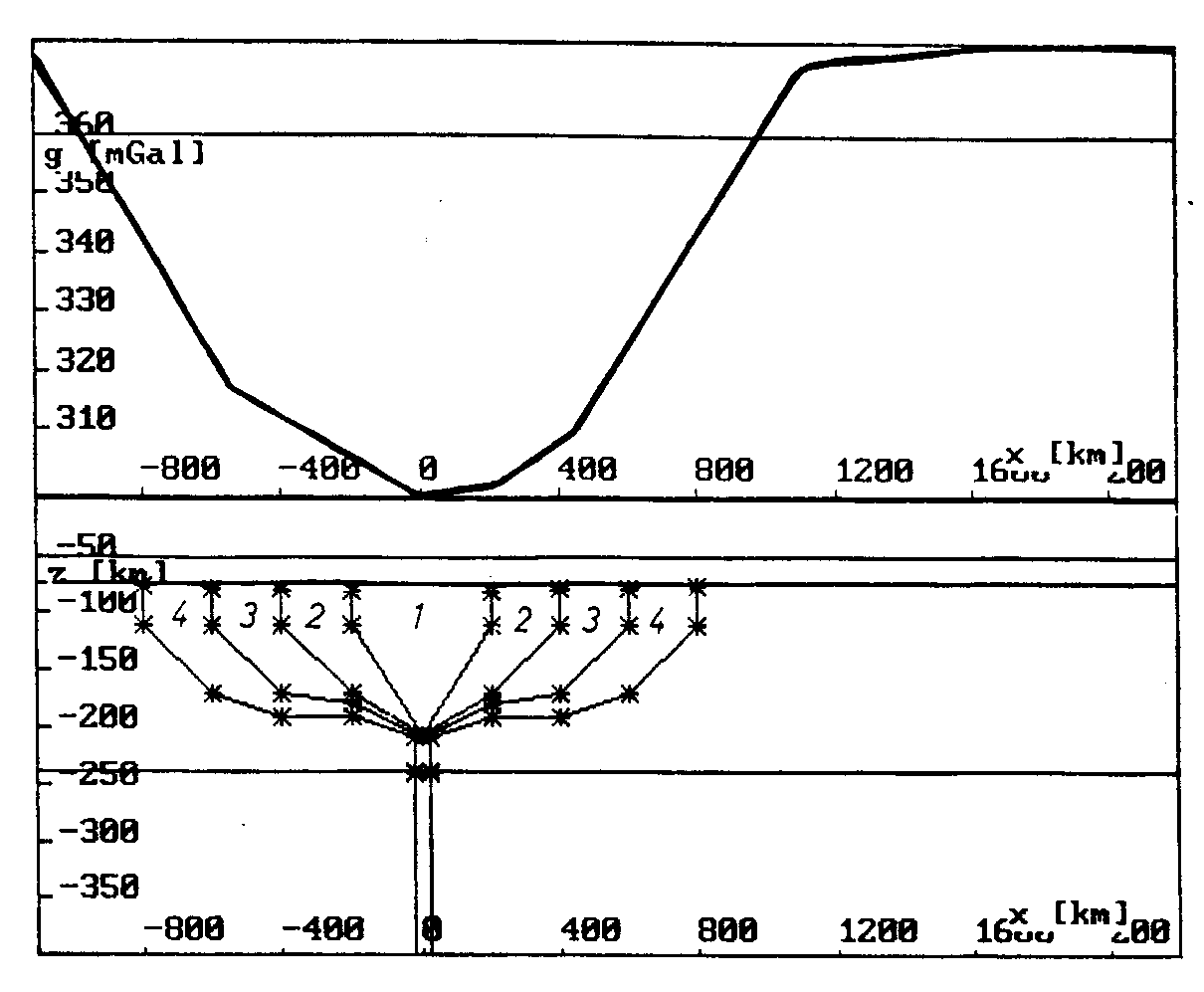
Abb. 42. Profilschnitt durch die Geometrie einer Mantel-Plume-Struktur,
die in ineinander liegende Temperatur- und damit Dichtebereiche
aufgeteilt ist. "1" stellt den innersten und "4" den äußersten
Bereich dar. "2" und "3" sind Abstufungen. Die angegebene Mo-
dellschwere gilt für eine über alle Bereiche konstante Dichte-
differenz zwischen Plume und umgebendem Material von -0,02
g/cm
Ein Profil durch das Zentrum der Struktur mit ihrer Geometrie zeigt Abb. 42, zugehörige Modellschwerefelder die Abb. 43a,b. Die in Abb. 43 gezeigten Modelle wurden mit dem Programmsystem "IGAS" von Prof. Dr. H.-J. Götze von der FU Berlin erstellt. Genauere Informationen zu der 3D-Schweremodellierung mit "IGAS" nach Götze und Lahmeyer (1988) findet der Leser in den Kap. 8.1.1. und Kap. 9.1.. Die 3D-Rechnungen haben gegenüber den 2D-Rechnungen den Vorteil, daß Effekte durch Strukturen in die Modellschwere mit einbezogen werden, die neben einer 2D-Profillinie liegen und damit das 2D-Ergebnis verfälschen. Diese Fehlerquelle liegt im 3D-Fall nicht mehr vor. An dieser Stelle sollen kurz die Einflüsse der oben gelisteten möglichen Eigenschaften der Mantel Plumes diskutiert werden.
Die Skizze in Abb. 44 illustriert den Zusammenhang zwischen Größe, Tiefenlage und Form des Störkörpers hinsichtlich seiner an der Oberfläche meßbaren Schwerewirkung. Danach liefern flacher liegende Strukturen kleiner Amplitude und großer Wellenlänge ein Signal, das dem tiefer liegender Strukturen großer Amplitude und kleiner Wellenlänge entspricht. Damit lassen sich viele Eigenschaften möglicher Mantel-Plume-Strukturen gravimetrisch eindeutig nicht herausarbeiten. Vielmehr werden Annahmen über die Mantel-Plume-Struktur hinsichtlich ihrer Größe, Tiefenlage und Form hineingesteckt, deren Schwerewirkung hier ermittelt werden soll. Auf die-se Weise läßt sich eine Abschätzung machen, ob denn überhaupt die Mantel-Plume-Struktur, wie sie in den verschiedenen theoretischen Modellrechnungen betrachtet wird, in der angegebenen Weise existieren kann.
Grundlage der Modellrechnungen in der vorliegenden Arbeit bildet eine Mantel-Plume-Struktur, die im wesentlichen die Abmessungen nach Abb. 42 hat. Dieser Mantel Plume weist eine relativ dünne Auftriebszone auf und liegt mit seiner Obergrenze in etwa 75 km bis 80 km Tiefe an der Lithosphärenbasis. Die pilzhutförmige Verbreiterung im Sublithosphärenbereich weist eine Ausdehnung von 1500 km auf. Die Dicke des Pilzhutes beträgt um die 100 km. Diese die Plume-Geometrie bestimmenden Werte werden auch durch die tomographischen Ergebnisse nach Abb. 23 unterstützt. Es hat sich gezeigt, daß die Form des Aufstiegskanals keine nennenswerten Beiträge zur Schwere liefert. Dieser Bereich des Mantel Plumes liegt bereits so tief, daß dies, gemessen am übrigen Beitrag, in den Hintergrund gerät. Es ist klar, daß die Tiefenlage und die Dicke des Pilzhutes einen größeren Einfluß auf die Modellschwere hat. Aber dies sind gerade die Parameter, die im Rahmen der späteren Anpassung der Modellschwere an gemessene Werte bestimmt werden sollen.
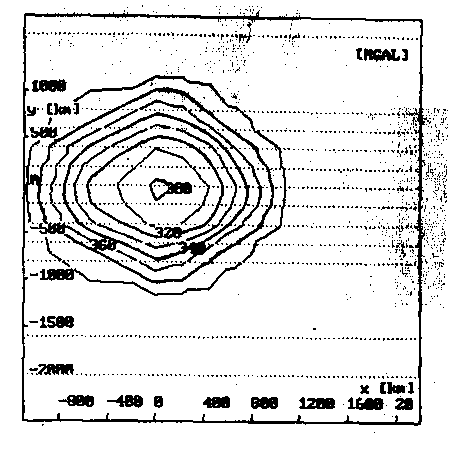
Die Dichteverteilung und damit die Temperaturverteilung im Inneren des Mantel Plumes wird einerseits konstant mit einem Dichtekontrast von -0,02 g/cm3 angenommen (Abb. 43a), andererseits wird die Abstufung gemäß Abb.
a)
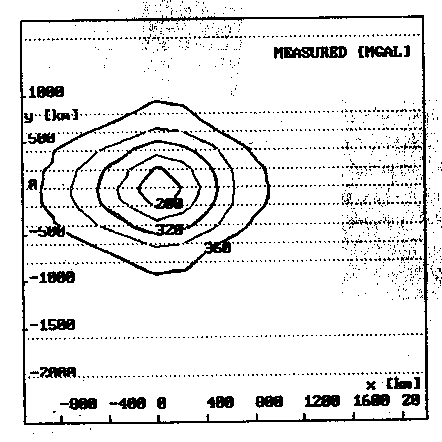
b)
Abb. 43. Schwerewirkung der 3D-Mantel-Plume-Struktur aus Abb. 42 für
verschiedene Dichtestrukturen:
a. Plume mit einer relativen Dichte von -0,02 g/cm
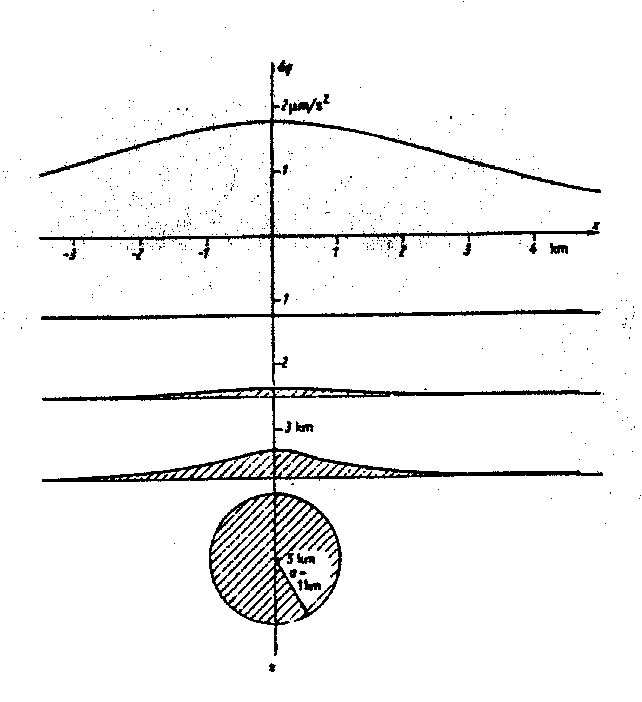
Abb. 44. Mehrdeutigkeit der Interpretation gravimetrischer Daten am Bei-
spiel der Schwerewirkung einer Kugel (Dichtedifferenz 1000
kg/m, Mittelpunktstiefe 5 km), die auch auf je eine der äquiva-
lenten Schichten in 1,25 km, 2,50 km sowie 3,75 km Tiefe zu-
rückführbar wäre (aus Militzer und Weber, 1984).
42 vorgenommen, so daß im innersten Bezirk eine Dichtedifferenz von -0,04 g/cm3 und im äußersten Bezirk eine Differenz von nur noch -0,01 g/cm3 gegenüber der Umgebung des Plumes vorliegt (Abb. 43b). Die Ergebnisse aus Abb. 43 zeigen, daß auch dies nur einen insofern zu beachtenden Einfluß auf die Modellschwere ausübt, daß die Amplitude und die Wellenlänge der Anomalie für den Fall einer abgestuften Temperaturverteilung (Abb. 43b) gegenüber dem konstanten Fall (Abb. 43a) etwas geringer ausfallen.
Dies kann aber leicht durch eine veränderte Geometrie des Plumekörpers ausgeglichen werden, so daß mit einer konstanten Dichte des Plumes gerechnet werden kann. Eine komplette Dichtedifferenzerhöhung oder -erniedrigung würde die Schwerewirkung um einen entsprechenden konstanten Faktor erhöhen oder vermindern. Bei den späteren Modellrechnungen soll jedoch aufgrund obiger Diskussionsergebnisse mit einer negativen Dichtereduktion von -0,02 g/cm3 gerechnet werden, so daß hier keine weitere Variable zur Verfügung steht. Aus Abb. 43 ergibt sich eine zu erwartende Schwereanomalie mit einer Amplitude von mehr als 60 mGal und einer halben Wellenlänge von mehr als 2000 km.
zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite