zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite
6. Aufbereitung der Daten für den Hawaii-Mantel-Plume-Hot-Spot
Im vorangegangenen Kapitel wurden Daten über Hawaii zusammengefaßt und der Stand der geophysikalischen Forschung über Hawaii und Mantel Plumes allgemein dargelegt, um damit eine Grundlage für die zu erarbeitenden Dichtemodelle in der vorliegenden Arbeit zu schaffen. In diesem Kapitel werden diejenigen Schritte dargelegt, die als Vorbereitung für das eigentliche Modellieren erforderlich sind. Hier erfährt der Leser einiges über die anfallenden Probleme bei der Bearbeitung der Daten und kann damit die Güte der Ergebnisse besser einschätzen. So sind z.B. die Freiluft- und bathymetrischen Daten aus Abb. 33 und Abb. 36 schon einem "Processing" unterworfen worden, das die Qualität der Daten beeinflußt.
6.1. Datenreduktion
Freilich wäre der Idealfall ein lückenloses, analoges Datenfeld der zu messenden Größe über das gesamte Meßgebiet. Aufgrund der anfallenden Datenmenge ist dies jedoch nicht zu realisieren. Vielmehr verlangt die digitale Datenverarbeitung, mittels derer in relativ kurzer Zeit komplexe Rechnungen ausgeführt werden können, die Eingabe diskreter Werte. Aufgrund des limitierten Speicherplatzvermögens und damit die Rechenzeit sich in Grenzen halten kann, können nur ein Bruchteil der Meßwerte in die Auswertung mit eingehen. Es ist daher von großer Wichtigkeit, nach welchen Kriterien man diesen Teil der Meßwerte aussucht. Dies richtet sich i. a. nach den Anforderungen, die bei der Auswertung gestellt werden. Auf jeden Fall ist eine Datenreduktion erforderlich, die den Informationsgehalt der Meßreihe hinsichtlich der beabsichtigten Auswertung nicht oder so gering wie möglich schädigt.
Zunächst einmal bedarf es einer Erläuterung der Daten, die in den Abb. 33 und Abb. 36 dargestellt sind. Da als Ziel eine 3D-Modellierung des regionalen Umfeldes des Hawaii-Mantel-Plume-Hot-Spots angestrebt wird, muß zunächst einmal das zu betrachtende Gebiet festgelegt werden. Aus Abb. 35 ist ersichtlich, welche Strukturen im zu betrachtenden Gebiet liegen sollten. Danach ist als Untersuchungsgebiet eine Region ausgewählt worden, die
im Norden durch den 40. nördl. Breitengrad,
im Süden durch den 10. nördl. Breitengrad,
im Osten durch den 140. westl. Längengrad und
im Westen durch den 175. östl. Längengrad begrenzt ist.
Diese Region ist durch den Kasten in Abb. 35 hervorgehoben. In dieser Region ist, wie aus Abb. 33 und Abb. 36 ersichtlich, das Gebiet der Hawaii-Inseln, der Hawaii-Schwelle und eines von Hawaii offenbar unbeeinflußten Bereichs um die Schwelle herum enthalten. Damit ist sowohl die zu untersuchende Struktur selbst als auch das Umfeld, um eine Abgrenzung zu ungestörtem Terrain durchführen zu können, berücksichtigt. Die Abtastrate für die Felddaten aus Abb. 33 und Abb. 36 beträgt fünf Minuten. Damit liegen pro Gradquadrat 144 Meßpunkte vor. Da sich der Abstand der Meridiane polwärts verjüngt, rücken die Meßwerte in ihrer geographischen Lage längs eines Breitenkreises polwärts immer enger zusammen. Die Quelle für die Daten aus Abb. 33 und Abb. 36 sind die Satellitenmessungen SEASAT, die längs der entsprechenden Flugbahnen gemacht wurden. Diese Meßreihen weisen längs ihrer Bahn hohe Datendichten auf, aber zwischen den Bahnen liegen keine Werte vor. Dabei betragen die Abstände zwischen den Bahnen oft mehr als ein Grad. Ferner stimmen die Werte an Kreuzungspunkten einzelner Bahnen nicht immer überein, so daß entsprechende Korrekturen angebracht wurden (z. B. Liang, 1983). Die SEASAT-Daten liegen in Form eines 5 x 5 - Minuten Grids vor, so daß die SEASAT-Rohdaten, die längs der Flugbahnen vorliegen, größtenteils durch Interpolation in ein Grid umgesetzt worden sind (Liang, 1983). Es ist klar, daß dieser Datensatz damit keine sinnvolle Information mehr aufweist, die in Wellenlängenbereichen liegen, die niedriger sind als die Meßdichte. Der Meßpunktabstand entlang eines Profiles beträgt ca. 6,8 km, der Abstand zweier Orbits vermag bis zu 100 km betragen. Die Auflösungsgrenze für durch SEASAT-Daten erfaßte Strukturelemente beträgt 35 km (Tapley et al., 1982; Marks und Sailor, 1986). Damit eignen sich diese Daten schon einmal nicht zur Untersuchung kurzwelliger Elemente. Aber dies ist hier auch nicht beabsichtigt. Vielmehr interessieren die langwelligen Strukturen. Informationen über diese Strukturen sind in den Daten damit noch vorhanden.
Die eigentliche Datenreduktion erfolgt jedoch erst. Die bereits besprochene Reduktion behandelte lediglich das Erstellen eines Ausgangsdatensatzes (SEASAT-Grid) aus Meßdaten (SEASAT-Orbits). Diese nun vorliegenden Meßdaten (SEASAT auf 5 x 5 - Minuten-Grid interpoliert) müssen nun weiter reduziert werden, um Rechenzeiten und Speicherplatzbedarf auf ein verträgliches Maß zu bringen. Die zu untersuchende Region soll dabei durch ein gleichmäßiges Grid, das etwa 1000 Datenpunkte aufweisen darf, repräsentiert werden. Der SEASAT-Datensatz für das Untersuchungsgebiet umfaßt 540 x 360 Datenpunkte. Diese Anzahl wird auf 45 x 30 Punkte reduziert. Dabei liegt nunmehr eine Datendichte von einem Wert pro Grad vor. Um dies zu erreichen, kann man verschiedene Methoden anwenden. Bei der Auswahl einer Methode ist darauf zu achten, daß die für die weitere Bearbeitung wichtige Information nicht verloren geht. Folgende Methoden der Datenreduktion sind möglich:
1. einfach in x- und y- Richtung nur jeden 12. Wert in die neue Datei aufnehmen,
2. benachbarte Werte der Originaldatei durch geeignete Mittelwertbildung zusammenfassen,
3. in Gebieten erhöhter Informationsdichte eine höhere und in Gebieten verminderter Informationsdichte eine verringerte Datenanzahl übernehmen.
Das 3. Verfahren ermöglicht eine möglichst genaue Informationsübertragung in eine weniger umfangreiche Datei. Jedoch liegt dabei kein konstantes Grid mehr vor. Dies erschwert die schnelle Weiterbehandlung der Daten. Diese Methode empfiehlt sich bei der Darstellung lokal auftretender, kurzwelliger Strukturen, die extensiv über das regionale Gebiet verbreitet sind. Da in der vorliegenden Arbeit aber insbesondere langwellige Strukturen von Wichtigkeit sind, kann nach Verfahren 1 oder 2 vorgegangen werden. Hier erhält man als Ergebnisdatei ein konstantes Grid.
Verfahren 2 ist auch komplexerer Natur. Es gibt verschiedene Mittelwertbildungen, um zu einer reduzierten Datei zu kommen. Dabei ist u. a. die Anzahl der einzubeziehenden benachbarten Werte (Fenster) geeignet festzulegen. Hierbei ist zu beachten, daß die Mittelwertbildung bereits eine Art "Filter" darstellt. Es werden diejenigen Strukturen ausgefiltert, deren Wellenlänge kleiner als der Mittelwertradius, d. h. der Entfernung, bis zu der noch Werte in den Mittelwert eingehen, ist. Außerdem weist diese Methode Randeffekte durch dort fehlende Werte auf. Aus diesem Grunde kann schließlich auch auf die Vorteile dieser Methode verzichtet werden und ganz elementar nach Methode 1 vorgegangen werden. Auf diese Weise sind die Daten der Abb. 33 und Abb. 36 reduziert worden, wie es die Abb. 45 und Abb. 46 zeigen.
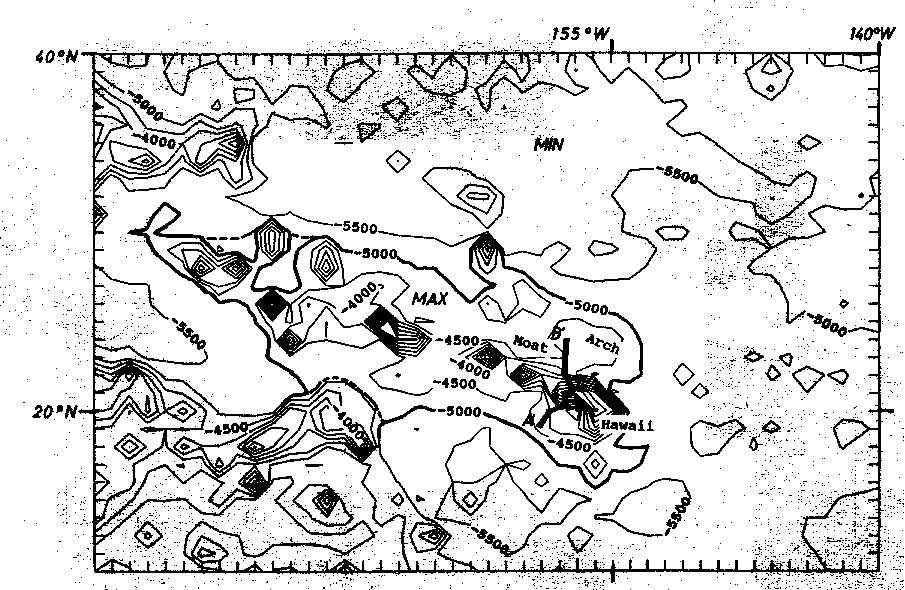
Im folgenden wird der Informationsgehalt der so entstandenen Datensätze verglichen, um zu zeigen, daß für die Zwecke der vorliegenden Arbeit die reduzierte Datenmenge zu keinen Fehlern führt. Die Reduktion der Datendichte führte dazu, daß lokale Strukturen wie kleine Seamounts aus Abb. 33 größtenteils verschwanden. In diesem Sinne liegt bereits eine Filterung zugunsten der langwelligeren Strukturen vor. Lediglich dort, wo die Abtastrate genau auf einen Seamount fiel, ist dieser in die reduzierte Datenmenge übernommen worden. Damit sind vereinzelte Lokalstrukturen doch noch im reduzierten Datensatz vorhanden. Da sie im allgemeinen nur durch ein bis zwei Werte charakterisiert sind, ist ihre genauere Form und Ausdehnung verfälscht. Die Dichte des verwendeten Datensatzes wird bei den Darstellungen aus Abb. 33, Abb. 36, Abb. 45 und Abb. 46 durch die Striche der Umrandung repräsentiert. Die im östlichen Drittel des Untersuchungsgebietes gelegenen Transformstörungen sind bei der Datenreduktion aufgrund ihrer "Schmalheit" ebenfalls verlorengegangen. Erhalten geblieben sind alle übrigen Strukturen. Wie der Vergleich von Abb. 33 mit Abb. 45 sowie Abb. 36 mit Abb. 46 zeigt, sind lediglich die genaueren Umrisse einzelner Strukturen nicht mehr so deutlich. Jedoch ist die Hawaii-Schwelle, markiert durch die 5000m-Tiefenlinie, in Abb. 33 und Abb. 45 sowie die korrespondierende Freiluftanomale (Nullinie) in Abb. 36 bzw. Abb. 46 klar ersichtlich. Form, Amplitude und Wellenlänge der Schwelle sind übertragen worden. Auch die Dimensionen der Hawaii-Kette sind bei den bathymetrischen Daten übertragen worden.
Die Verteilung der lokalen Maxima und Minima der Freiluftschwere in unmittelbarer Umgebung um die Hawaii-Kette ist sowohl in Abb. 36 als auch in Abb. 46 ersichtlich. Die Abb. 33, Abb. 36, Abb. 45 und Abb. 46 enthalten die Lage des Profils, entlang dessen die in Kapitel 5 diskutierten Krustenmodelle von Watts et al. (1985) und Lindwall (1988) entwickelt worden sind. Hier kann man den Verlauf von Bathymetrie und Freiluftschwere im Zusammenhang mit der gesamten Region erkennen. Die Hawaii-Inseln und -Seamounts selbst weisen ein starkes Maximum der Freiluftanomalie auf. Die Hawaii-Kette ist von einem linearen lokalen Minimum umrundet, daß besonders an der Stirnseite der Kette im Osten ausgeprägt ist (Abb. 36 und Abb. 46).

Abb. 45. Die Bathymetrie der Hawaii-Schwelle mit reduzierter Datenmenge.
Der Isolinienabstand beträgt 500 m, die 5000m - Tiefenlinie ist
als Schwellencharakteristikum hervorgehoben. Eingetragen ist
die Lage des den Abb. 38 und Abb. 39 zugrundeliegenden Profiles
A'B'.
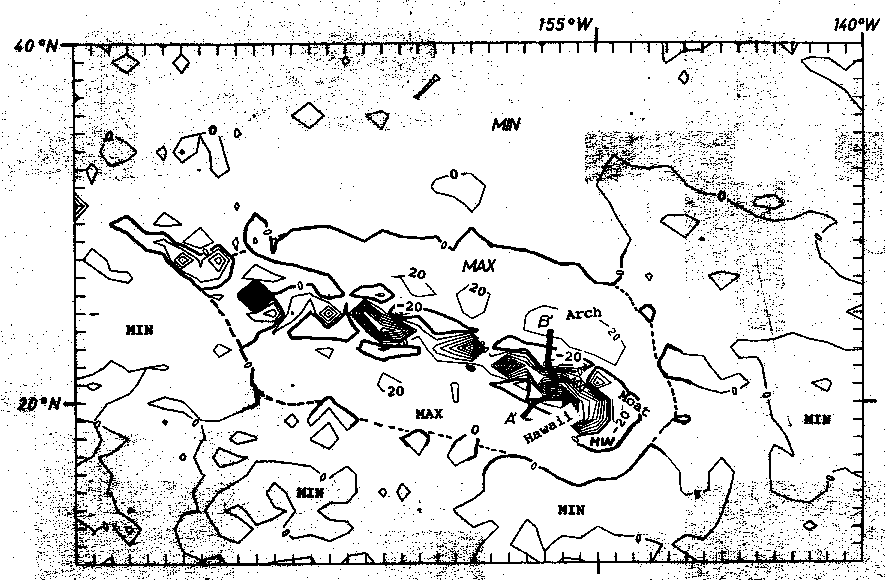
Abb. 46. Die Freiluftschwere der Hawaii-Schwelle mit reduzierter Daten-
menge. Der Isolinienabstand beträgt 20 mGal. Die Nullinie ist
als Schwellencharakteristikum hervorgehoben. Eingetragen ist
die Lage des den Abb. 38 und Abb. 39 zugrundeliegenden Profiles
A'B'.
An dieser Stelle muß nochmals darauf hingewiesen werden, daß zwar ein konstantes Datengrid vorliegt, die Datendichte sich längs eines Breitenkreises polwärts, also nach Norden hier, erhöht. Dies liegt an dem sich verringernden Abstand der Meridiane, entlang derer "gesampelt" worden ist. Das Gebiet liegt zwischen dem 10. und 40. Grad nördlicher Breite. Damit ergeben sich breitenabhängige Datenabstände in Ost-West-Richtung. Auf dieses Problem wird im Rahmen der 3D-Modellierung in Kapitel 8 noch näher eingegangen. Dann wird der Ursprung und ein mittlerer Datenabstand ermittelt, auf dessen Grundlage der Vergleich von Modell- und gemessener gefilterter Bouguerschwere durchgeführt werden soll.
Überdies ist noch die Erdkrümmung hinzuzuziehen. Diese liegt im betrachteten Gebiet bei einem maximalen Wert von 45 Grad im äquatorialen Bereich in Ost-West-Richtung und bei 30 Grad in Nord-Süd-Richtung. Da jedoch regional ausgedehnte Strukturen in größerer Tiefe (bis zu mehr als 100 km) modelliert werden sollen, ist nach Detrick und Crough (1978) sphäri-sches Rechnen nicht erforderlich. Für die späteren Berechnungen können diese Effekte somit problemlos vernachlässigt werden, da es zunächst um die Gewinnung einer qualitativen Aussage geht.
6.2. Filterung synthetischer Daten
Da sich die vermutete Mantel-Plume-Struktur im langwelligen Bereich des Schwerefeldes bemerkbar machen müßte, wird es erforderlich, die Daten dahingehend zu filtern. In der Literatur findet man eine Vielzahl von Methoden, mit denen man die Trennung des Schwerefeldes und der Topographie bzw. Bathymetrie nach regionalen und lokalen Anteilen durchführen kann. Diese Zielsetzung läßt sich auf verschiedene Arten umsetzen:
- Wellenlängenfilterung
- Feldfortsetzung
- graphische Regionalfeldbestimmung
- Mittelwertbildung aus Datenpunkten in der Umgebung
- Tschebyschev-Polynom-Approximation.
Alle diese Methoden liefern aus einem Ausgangsdatensatz selbst dann unterschiedliche Filterergebnisse, wenn jede Methode entsprechend der gesetzten Zielsetzung, hier Trennung langwelliger Anteile, eingesetzt wird. Die Frequenz-Wellenlängenfilterung bietet sich für das Problem vom Namen her an. Sie weist jedoch schwerwiegende Nachteile gegenüber anderen, in der Regel mathematisch einfacher aufgebauten Methoden auf. So bewegt sich die wichtigste auszufilternde Struktur, die Hawaii-Schwelle, in einem Wellenlängenbereich, der größenordnungsgemäß im Bereich der Meßgebietsgröße liegt. Damit tritt das Problem des Randeffektes in den Vordergrund. Um diesen zu minimieren, müßte entweder das zu betrachtende Gebiet vergrößert sein oder eine geeignete Feldfortsetzung im Datensatz eingeschlossen sein. Beides erfordert eine derart große Datenmenge, daß dies als nicht praktikabel erscheint. Darüber hinaus weist diese Filterart den weiteren Nachteil auf, daß man im Ergebnisdatenfeld nicht unmittelbar ersehen kann, welche Strukturen möglicherweise Artefakte sind. Außerdem hängt die Ergebnisfunktion in starkem Maße von der genauen Wahl der Werte und der Art der Filtergrenzen ab. Die Problematik gefilterter Daten mittels der Frequenz-Wellenlängenfilterung trat auch bei anderen Autoren auf, die sich mit gefilterten Geoid-Karten auseinandersetzten (z. B. Vogt et al., 1984; Bowin et al., 1984; Jung und Rabinowitz, 1986 und Cazenave et al., 1988). Überdies ergeben sich allgemeine Probleme bei der Darstellung gefilterter Daten, auf diese Probleme gehen z. B. McNutt und Shure (1986) und Sleep (1990) näher ein.
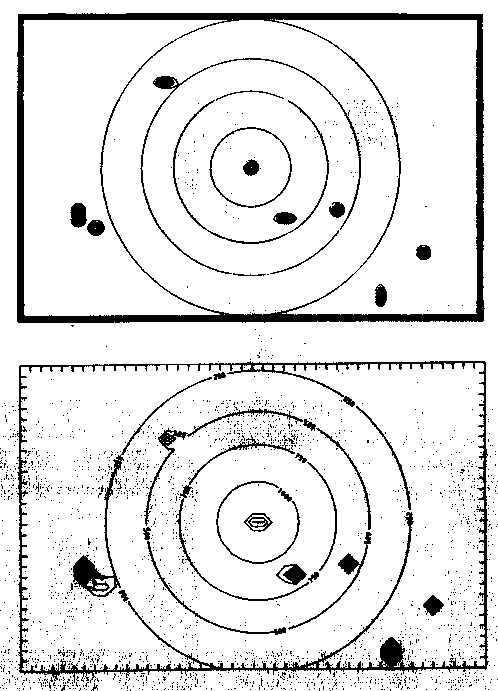
Zur Beurteilung des Leistungsvermögens der verschiedenen Processing-Schritte wie Datenausdünnung und der Filtermethoden wird auf einen synthetischen Datensatz zurückgegriffen. Dieser simuliert die idealisierte bathymetrische Struktur eines mutmaßlichen Mantel-Plume-Hot-Spots. Dazu gehören eine Schwelle regionalen Ausmaßes und dieser Schwelle aufgesetzte, lokale Vulkangebäude. Die topographische Anomalie (Schwelle) läßt sich durch Gauß-Funktionen beschreiben (Detrick und Crough, 1978; Monnereau und Cazenave (1990). Dehnt man diese Erkenntnis auch auf die Vulkane selbst aus, so läßt sich eine synthetische Bathymetrie durch einfache Addition verschieden parametrisierter Gaußfunktionen darstellen. Auf diese Weise sind die Daten in Abb. 47 erstellt worden.
Die Frequenz-Wellenlängenfilterung wurde aufgrund obengenannter Probleme als nicht geeignet erachtet. Die Mittelwertbildung, die eine Verfeinerung der Mittelwertbildung aus der Datenausdünnung darstellt, liefert Ergebnisse, deren physikalische Aussagekraft hinsichtlich langwelliger Strukturen problematisch ist. Aussagefähige Resultate lassen sich jedoch mit der Methode der Polynomapproximation nach Tschebyschev erzielen. Diese Methode liefert eine Darstellung der langwelligen Strukturen ohne die möglicherweise vorhandenen, aber verborgenen Nebeneffekte, die sich aus der rechnerischen Umsetzung komplexer mathematischer Randbedingungen unerkannt einschleichen können. Da mögliche Artefakte damit auszuschließen
a)
b)
Abb. 47. Synthetischer Datensatz, bestehend aus simulierten Vulkanen als
lokaler und der Schwelle als regionaler Beitrag zur Topogra-
phie.
a. vollständige 540 x 360 Punkte,
b. reduzierte 45 x 30 Punkte umfassende Datenmenge.
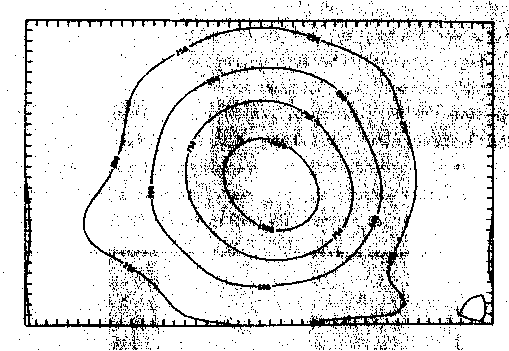
a) Grad 7
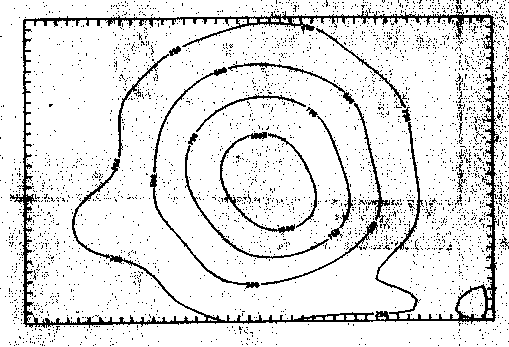
b) Grad 8
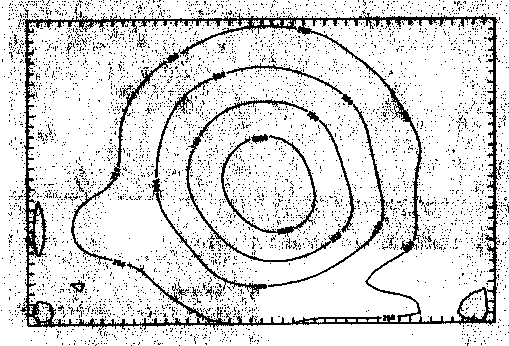
c) Grad 9
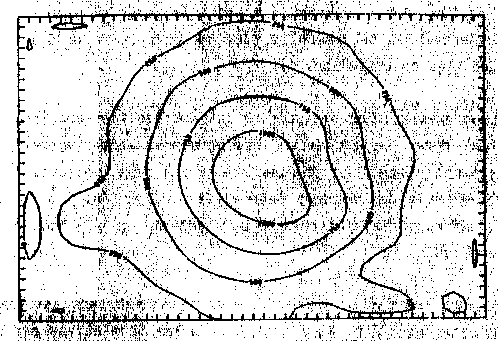
d) Grad 10
Abb. 48. Ausgefilterte, regionale Anteile der synthetischen Daten durch
Tschebyschev-Anpassung vom Grad 7, 8, 9 und 10.
sind, kann das Ergebnis gänzlich physikalisch interpretiert werden. Die kurzwelligen Strukturen ergeben sich aus der Differenz von Originalfelddaten und der Daten des langwelligen Feldes. Für die 3D-Modellierung werden die nötigen langwelligen Daten mittels der Tschebyschev-Polynom-Approximation gewonnen. Die nachfolgenden Abb. 47 und Abb. 48 veranschaulichen die Bearbeitung des synthetischen Datensatzes mit der Tschebyschev-Approximation.
Es zeigt sich, daß das gewählte Datenausdünnungsverfahren die erwarteten Resultate liefert. Es geht keine wichtige Information hinsichtlich der langwelligen Analyse verloren (Abb. 47). Die Tschebyschev-Approximation zeigt die langwelligen Anteile. Die lokalen Anteile konnten gut weggefiltert werden. Der Vergleich der Grade, bis zu welchem approximiert wurde, zeigt, daß und in welcher Weise mit zunehmendem Grad die Lokalanteile langsam zunehmen (Abb. 48).
6.3. Berechnung der langwelligen Bougueranomalie um den Hawaii-
Mantel-Plume-Hot-Spot
Die über der Hawaii-Schwelle gemessenen Freiluftwerte gemäß Abb. 36 bzw. Abb. 46 spiegeln im wesentlichen die bathymetrischen Verhältnisse nach Abb. 33 bzw. Abb. 45 wider. Um erste Aussagen über den sublithosphärischen Bereich zu bekommmen, bietet es sich an, eine Bouguerschwerekarte des Gebietes zu erstellen.
Die Bouguer-Reduktion ergibt sich aus der Addition der Schwerewirkung des mit geeigneter Gesteinsdichte beschriebenen Wasserkörpers und der Freiluftschwere. Dabei ist zu beachten, daß der Freiluftwert bereits die Schwerewirkung des Wassers beinhaltet. Addiert wird also lediglich die Schwerewirkung eines Gesteinskörpers mit der um die Wasserdichte verminderten Dichte.
Die Berechnung der Schwerewirkung des Wasserkörpers aus den bathymetrischen Daten nach Abb. 45 führte Dr. Sabine Schmidt von der Arbeitsgruppe von Prof. Dr. H.-J. Götze vom Institut für Geologie, Geophysik und Geoinformatik der FU Berlin aus. Die Berechnung der Schwerewirkung geschah zunächst über das Massenlinienmodell nach Militzer und Weber (1984), Gl. 2.37:
hi'2
gTop = 2 . . . b2 . ____ ,
ri3
wobei gTop : Geländereduktion,
b : halbe Kantenlänge des Körpers in Abb. 49,
: Reduktionsdichte,
: Gravitationskonstante.
Die übrigen Parameter verdeutlicht die Abb. 49a,b.
Es wurden senkrechte Massenlinien genommen. Diejenige Massenlinie, die direkt unter dem zu berechnenden Aufpunkt (singulärer Punkt) lag, wurde dabei durch einen exakt berechneten Quader ersetzt. Für die Seitenlängen b wurde der halbe sphärische Abstand der Aufpunkte genommen, r war der sphärische Abstand vom Aufpunkt zur Massenlinie, h die Tiefe des Meeresbodens. Es wurde auch mit der exakten Quaderformel nach Ehrismann und Lettau (1971) gerechnet. Die gewonnenen Ergebnisse unterschieden sich von denen der obigen Näherung durch Massenlinien im Vergleich zu den benötigten Rechenzeitunterschieden unerheblich. Ein Reduktionsradius wurde nicht verwendet. Vielmehr wurden jeweils alle Topographiepunkte für alle Aufpunkte bestimmt. Damit ist der Rand "unterreduziert".
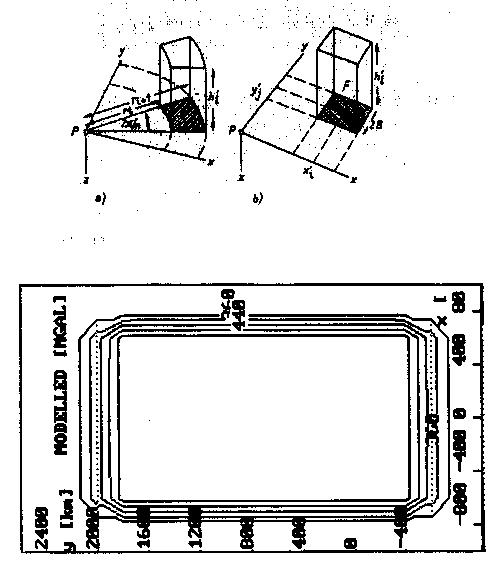
c)
Abb. 49. a,b) Elementarkörper zur Berechnung der Geländereduktion nach
Militzer und Weber (1984).
a) manuelle Berechnung, b) rechnergestützte Berechnung.
c) Schwerewirkung eines 2600 x 1400 x 5 km3 großen Modellqua-
ders zur Abschätzung des Randeffektes, der bei der Bouguer-
reduktion auftritt.
Für die Abschätzung dieses dabei auftretenden Randeffekts wurde die Schwerewirkung für einen Quader berechnet (vgl. Abb. 49c). Um die "Meßpunkte", an denen nach Abb. 59 die Modellschwere berechnet wird, benutzen zu können, umfaßt dieser Quader eine horizontale Ausdehnung von 2600 x 1400 km2, was der Größenordnung des Untersuchungsgebietes entspricht. Die vertikale Ausdehnung beträgt 5 km, was der mittleren ungestörten Meerestiefe im Untersuchungsgebiet entspricht. Die in Abb. 49c dargestellte Schwerewirkung dieses Quaders zeigt, daß der Randeffekt lediglich auf die randnahen Bereiche beschränkt bleibt. Abgesehen vom Randbereich tritt über dem gesamten Quaderbereich kein nennenswerter Schweregradient auf, so daß die Bouguerschwere nahezu randeffektfrei berechnet wurde.
Dieser Randeffekt betrifft somit im Untersuchungsgebiet lediglich zwei Grad und damit etwa zwei bis drei Gridpunkte der reduzierten Datenmenge. Diese Werte werden aus der Interpretation herausgenommen. Dies ist durch die in die Abb. 50 eingetragene Randeffektgrenze (gestrichelte Linie) hervorgehoben. Diese Linie zeigen alle nachfolgenden Abbildungen, die mit dem in der Abb. 50 dargestellten Ergebnis berechnet wurden. Diese Verringerung des Datensatzes schränkt die Aussagekraft des Ergebnisses nicht ein, da die Hawaii-Schwelle und ihre Umgebung davon nicht betroffen sind.
Die auf die oben beschriebene Weise errechnete Schwerewirkung des Wasserkörpers zeigt Abb. 50, wobei hier der Wasserkörper mit der mittleren Krustendichte von 2,95 g/cm3 angesetzt wurde. Die Reduktionsdichte beträgt 1,95 g/cm3, welches die Differenz aus der mittleren Krustendichte und der Wasserdichte ist. Die für die Berechnung nötige Bathymetrie entstammt der Abb. 49, die eine Reduktion der Daten nach Abb. 33 darstellt.
Während Abb. 46 kaum noch lokale Strukturen aufweist, finden sich diese noch in der Schwerewirkung des Wasserkörpers (Abb. 50). Dies hat folgende Ursachen. Zum einen sind durch die Datenreduktion beim Übergang von Abb. 36 auf Abb. 46 lokale Strukturen verlorengegangen, zum anderen liegt dies bei der SEASAT-Freiluftanomalie in der Natur der Messung. Die Original-SEASAT-Daten sind Geoidmessungen und unterdrücken damit die kleineren Wellenlängen. Während das Schweresignal eines Störkörpers quadratisch mit zunehmender Entfernung r abklingt (1/r2 - Abhängigkeit), nimmt das Geoidsignal hingegen nur linear ab (1/r - Abhängigkeit). Auf diese Weise verschwinden bereits systematisch Lokalstrukturen zugunsten von Anomalien größerer Ausdehnung. Darin manifestiert sich die Eigenschaft, daß das Geoid insbesondere tiefere und ausgedehntere Strukturen repräsentiert. Dies trifft jedoch nicht für die Messung der Bathymetrie zu. Hier mißt man nicht das Geoid (mathematische Oberfläche) und auch kein Feld, das es noch in der Umlaufbahn selbst gibt. Vielmehr ist die bathymetrische Funktion (physikalische Oberfläche bzw. Grenzfläche) in allen Höhen gleich bzw. längs der mathematischen Oberfläche des Körpers definiert, so daß es hier abgesehen von der Datenreduktion zu keinerlei weiteren in der Natur
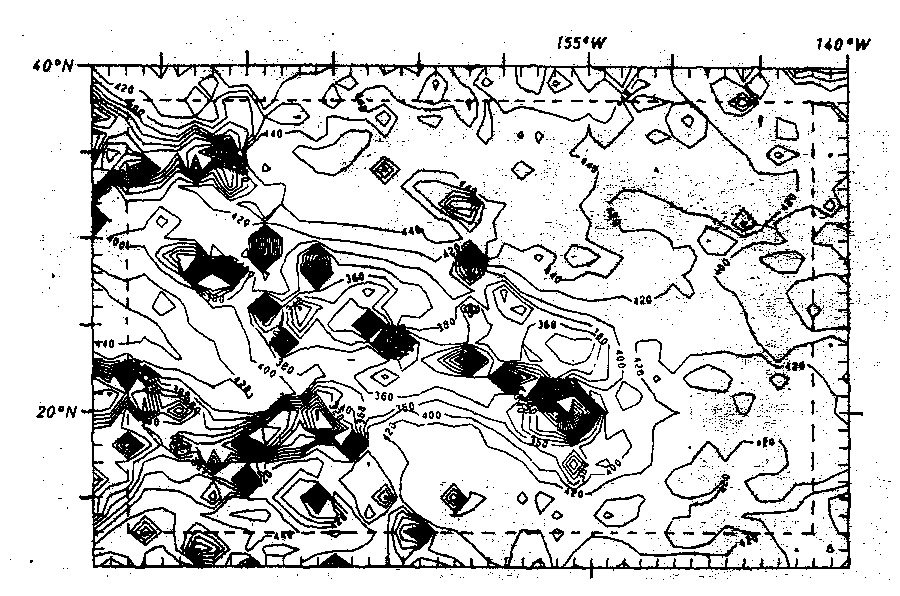
Abb. 50. Schwerewirkung des Wasserkörpers in mGal, gerechnet mit einer
mittleren Dichte von 2,95 g/cm
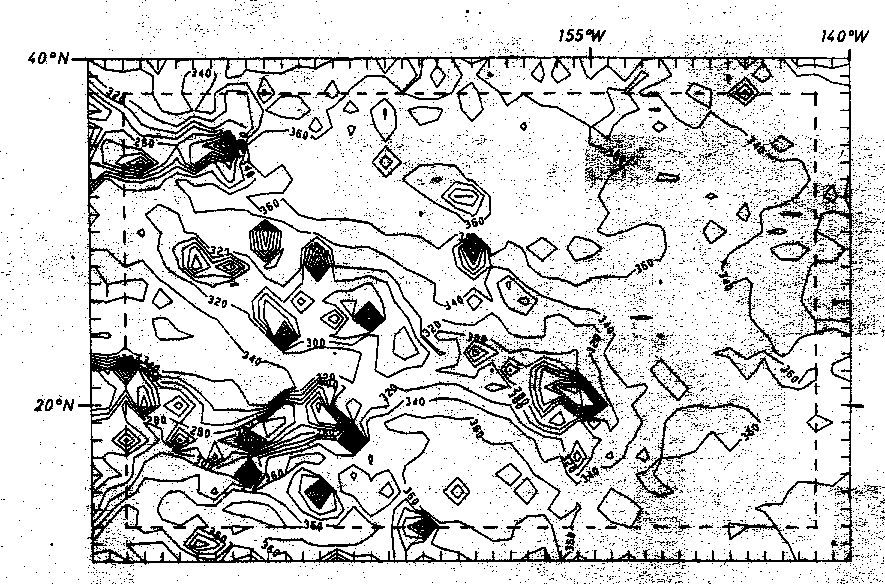
Abb. 51. Bouguerschwere-Karte der Hawaii-Schwelle, errechnet mit einer
Reduktionsdichte von 1,95 g/cm
der Messung liegenden Abweichungen mehr kommt. Da die Schwerewirkung des Wasserkörpers multiplikativ aus der Bathymetrie hervorgeht, wird die Wirkung sämtlicher in diesen Daten vorhandener Lokalstrukturen mit in den Schweredatensatz des Wasserkörpers übernommen. Auf diese Weise erhält man hier wesentlich mehr lokale Strukturen als in der Freiluftanomalie.
Die so berechnete Schwerewirkung, multipliziert mit dem entsprechenden Faktor, um die Gesteinsdichte der oberen Kruste zu modellieren, wird nun auf die Freiluftanomalie addiert. Dies ergibt dann die Bouguerschwere nach Abb. 51. Durch die einfache Addition wurden natürlich sämtliche durch die Wasserkörperschwereberechnung aufgetretenen Lokalanomalien eingestreut. Diese verfälschen den Erfolg der Bouguerreduktion. Diese liefert die erwarteten Ergebnisse nur in den langwelligeren Bereichen.
Um die kurzwelligen Störanteile zu beseitigen, und da ohnehin die Darstellung des langwelligen Feldes der Bougueranomalie gesucht ist, wird die Bougueranomalie zweidimensional gefiltert. Die Ergebnisse der Filter-
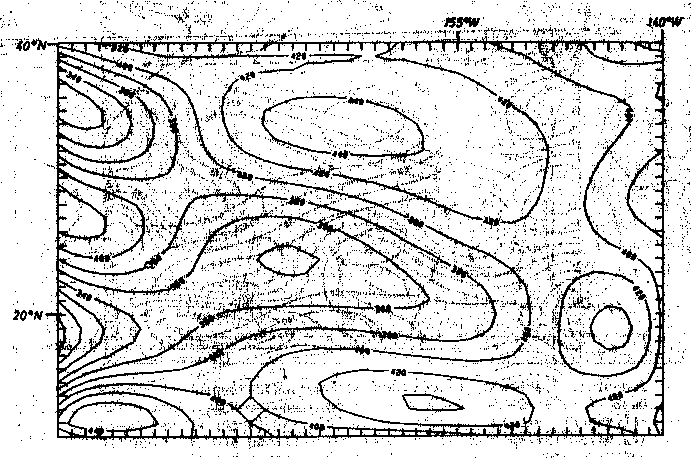
a) Grad 6
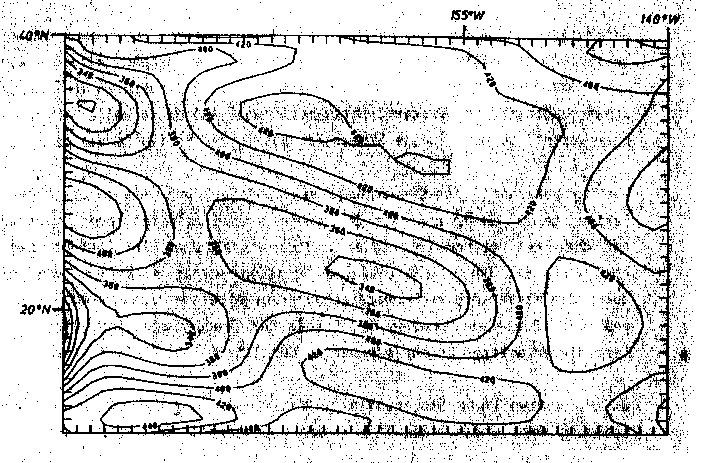
b) Grad 7
c) Grad 8
d) Grad 9
e) Grad 10
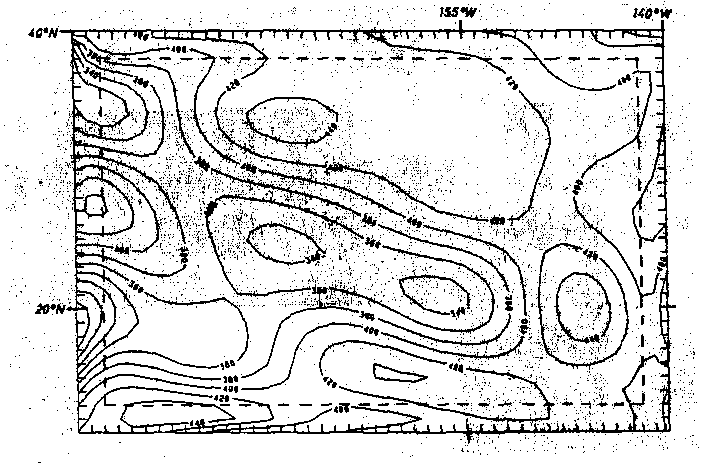
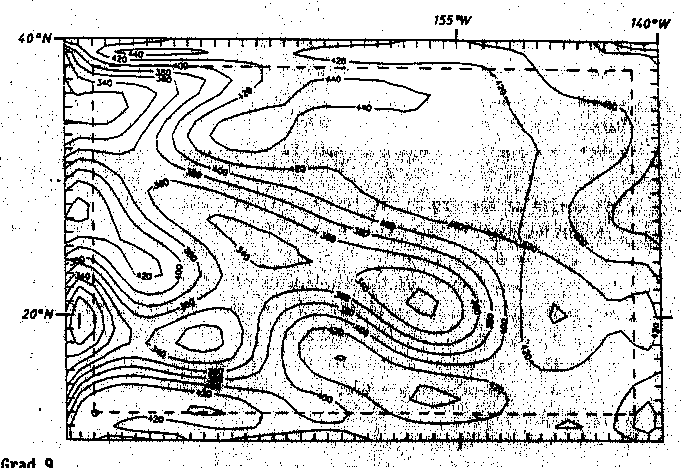
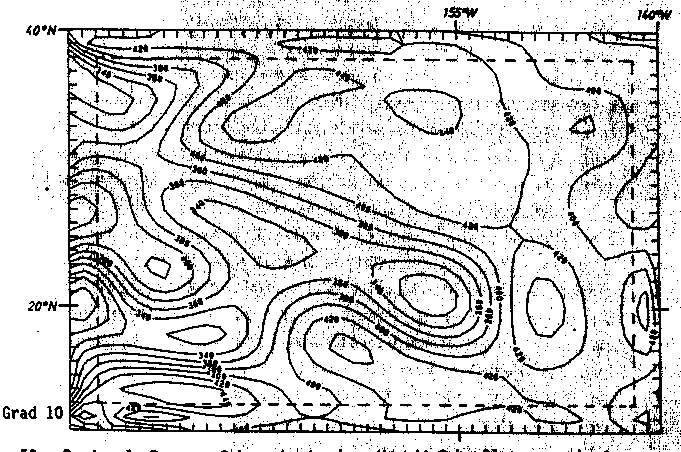
Abb. 52. Regionale Bouguer-Schwerekarte der Hawaii-Schwelle, errechnet
durch Tschebyschev-Anpassung mit a) Grad 6, b) Grad7, c) Grad
8, d) Grad 9 und e) Grad 10. Dies repräsentiert die langwelli-
gen Anteile. Die parallel zum Rand verlaufende gestrichelte Li-
nie markiert die äußerste Grenze des Einflusses rechnerischer
Randeffekte. Die Angaben sind in mGal.
güteuntersuchungen nach Kap. 6.2. haben gezeigt, daß sich für diese Problematik die Anpassung durch Tschebyschev-Polynome anbietet. Die besten Ergebnisse ergaben sich in Kap. 6.2. für n=7, 8, 9 und 10, so daß diese Darstellungen jetzt auf die Originaldaten angewendet wurden. Als Ergebnis erhält man die Darstellung nach Abb. 52.
Der Vergleich der Ergebnisse für die verschiedenen Grade der Polynomapproximation nach Tschebyschev zeigt, daß die Struktur der hawaiianischen langwelligen Bougueranomalie sehr gut für Grad 9 herausgearbeitet ist. Hier zeigt sich ein absolutes Minimum im vulkanisch noch aktiven Bereich der Inselkette. Ferner erkennt man deutlich die gestreckte Form der Anomalie, angeordnet parallel zum Streichen der Inselkette. Für die Modellrechnungen um das 3D-Dichtemodell wird auf die Darstellung der langwelligen Bouguerschwere vom Grad 9 als Vergleichsschwere zurückgegriffen (vgl. Kap. 8).
Der Vergleich der Ergebnisse nach Abb. 52 mit Abb. 53 zeigt eine weitgehende Übereinstimmung der langwelligen Bathymetrie mit der langwelligen Bougueranomalie im Bereich der Hawaii-Schwelle. Die negative Bougueranomalie verdeutlicht, daß im Bereich der Hawaii-Schwelle tieferliegende Massendefizite liegen müssen. Dies ist ein erster Hinweis auf eine existierende sublithosphärische Plumestruktur und/oder eine veränderte Lithosphäre verminderter Dichte. Die vergleichende Betrachtung der ungefilterten Bathymetrie (Abb. 45) mit der ungefilterten Bougueranomalie (Abb. 51) zeigt insbesondere, daß die Inselkette aus Ostsüdost kommend abrupt aufsteigt, ohne daß vorher eine regionale Schwellung vorliegt. Diese Beobachtung gilt nicht mehr für die Bougueranomalie des vor den Inseln liegendes Gebietes. Die Bougueranomalie sinkt bereits im weiteren Vorfeld der Inseln. Die regionale negative Bougueranomalie schmiegt sich in gleicher Weise um die gesamte Inselkette. Zieht man Abb. 33 hinzu, so erkennt man, daß diejenige Oberflächenstruktur, die man senkrecht zum Streichen der Inselkette gemäß den Abb. 38 und Abb. 39 erhält, nicht im Bereich vor der Inselkette zu finden ist. Das lokale Maximum der Meerestiefe ("Moat"), das parallel zum Streichen der Inselkette beiderseits derselben existiert, gibt es vor der Inselkette nicht in dieser ausgeprägten Form. Die Freiluftschwere (Abb. 36) weist in diesen Bereichen langgesteckte lokale Minima auf. Im Gegensatz zur Bathymetrie umschließt das die Inselkette umrahmende Minimum dieselbe auch an der Front im Ostsüdosten.
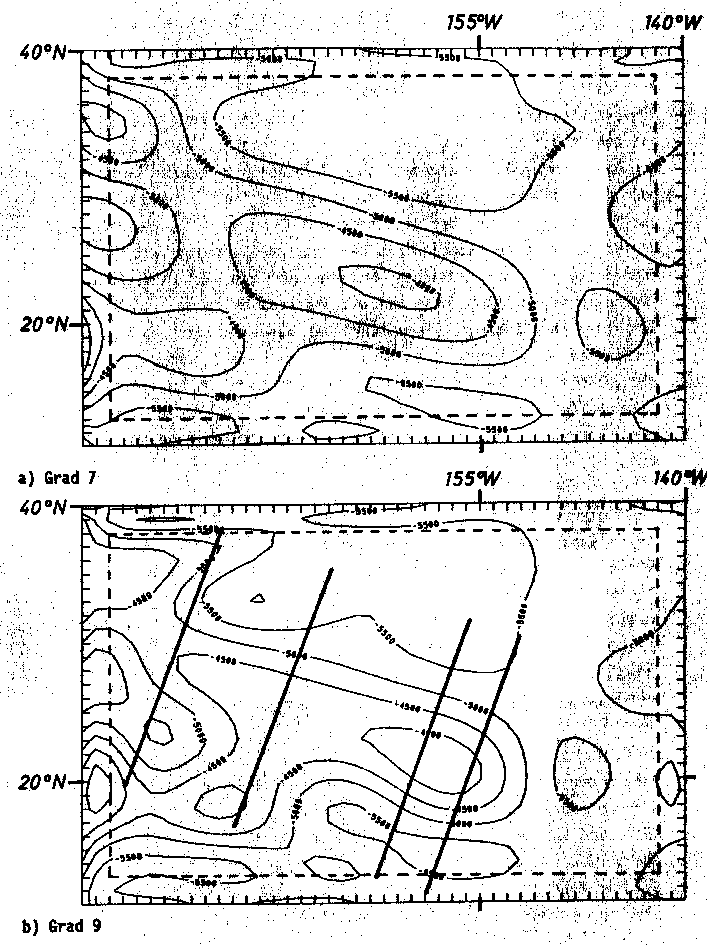
Abb. 53. Bathymetrische Karte der Hawaii-Schwelle, errechnet durch
Tschebyschev-Anpassung mit a) Grad 7 und b) Grad 9. Dies reprä-
sentiert die langwelligen Anteile. Die Angabe der Tiefen ist in
m. Die in b) eingetragenen Linien bezeichnen die Profile, längs
derer die in Abb. 74 dargestellte Massensummation berechnet
wurde.
An dieser Stelle sei eine allgemeine Bemerkung zur Güte berechneter Isolinienkarten und Filterungen durch Computeralgorithmen, die auf mathematischen Grundlagen beruhen, erlaubt. Die rechnergestützten Ergebnisse mögen zwar auf exakten mathematischen Prinzipien beruhen. Aber sie weisen deutliche Nachteile gegenüber graphischen und damit subjektiven Verfahren zur Bestimmung geeigneter Isolinien und Filterungen von Karten auf. So bleibt aufgrund der Komplexität der zugrundeliegenden Mathematik im Zusammenhang mit der endlichen Rechengenauigkeit und Randeffekten nicht zweifelsfrei, was Artefakte und was Information in den Daten darstellt. Bei spärlicher Datengrundlage führt das manuelle Zeichnen von Isolinien sicherlich zu genaueren Ergebnissen, da in diese Karten z. B. zusätzlich die geologischen Kenntnisse des Bearbeiters über das Auftreten bestimmter Landschafts- und damit Oberflächenformen eingehen. Derartige Qualitätsunterschiede von handgezeichneten und computergesteuerten Isolinienplänen werden z. B. in Smith und Wessel (1990) deutlich.
Die Filterung mittels graphischer Methoden führt in der Regel zu besseren Ergebnissen, die aber im Computerzeitalter der Verteidigung aufgrund ihrer subjektiven Natur leider nicht mehr standhalten. Daher müßte sich an dieser Stelle durchsetzen, die jeweilige zur Lösung der gestellten Problematik angemessene Methode zu benutzen. Eine subjektive Bearbeitung vermag oft bessere Ergebnisse zu erzielen, da der "Black-Box-Effekt" der oftmals benutzten Software hierbei nicht dazu beiträgt, möglicherweise physikalischen Unsinn zu produzieren, der dann auch noch interpretiert wird.
Sobald die zur Bearbeitung von Daten erforderliche Mathematik in ihrer Wirkung bzgl. der physikalischen Eigenschaften der Daten nicht mehr kalkulierbar ist, sollte in obigem Sinne auf bewährte Methoden zurückgegriffen werden. In diesem Sinne wählte der Autor der vorliegenden Arbeit z. B. die Tschebyschev-Polynom-Approximation für die Erkennung langwelliger Strukturen oder die einfache Datenreduktion ohne mathematische Zusätze.
zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite